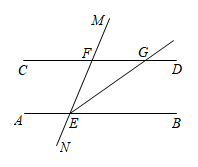2023年浙教版数学七年级下册全方位训练卷1.4平行线的性质
试卷更新日期:2023-01-12 类型:同步测试
一、单选题(每题3分,共30分)
-
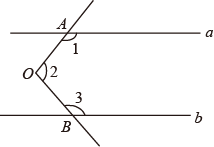
1. 下列说法中,错误的是( )A、两直线平行,同位角相等 B、对顶角相等 C、同旁内角互补,两直线平行 D、两条直线被第三条直线所截,内错角相等2. 如图,AB∥CD, , , 则的度数是( )
 A、30° B、40° C、50° D、45°3. 如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F的度数是( )
A、30° B、40° C、50° D、45°3. 如图,直线AB与CD相交于E,在∠CEB的平分线上有一点F,FM∥AB.当∠3=10°时,∠F的度数是( ) A、82° B、80° C、85° D、83 °4. 如图,直线 , 将含30°角的直角三角板ABC的直角顶点C放在直线b上,若 , 则的度数为( )
A、82° B、80° C、85° D、83 °4. 如图,直线 , 将含30°角的直角三角板ABC的直角顶点C放在直线b上,若 , 则的度数为( ) A、35° B、45° C、55° D、65°5. 如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上, , , 则下列结论错误的是( )
A、35° B、45° C、55° D、65°5. 如图,在三角形ABC中,点D,E,F分别在AB,AC,BC上, , , 则下列结论错误的是( )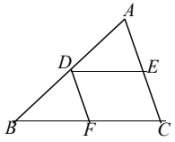 A、 B、 C、 D、6. ∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )A、 B、 C、 D、或7. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( )
A、 B、 C、 D、6. ∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )A、 B、 C、 D、或7. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( ) A、60° B、50° C、70° D、65°8. 如图,已知 , 平分 , 且 , 则与的关系是( )
A、60° B、50° C、70° D、65°8. 如图,已知 , 平分 , 且 , 则与的关系是( )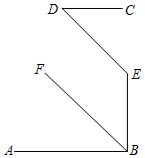 A、 B、 C、 D、9. 小明和小亮在研究一道数学题,如图 , , 垂足分别为E、D,G在上.
A、 B、 C、 D、9. 小明和小亮在研究一道数学题,如图 , , 垂足分别为E、D,G在上.小明说:“如果 , 则能得到”;
小亮说:“连接 , 如果 , 则能得到”.
则下列判断正确的是( )
 A、小明说法正确,小亮说法错误 B、小明说法正确,小亮说法正确 C、小明说法错误,小亮说法正确 D、小明说法错误,小亮说法错误10. 如图,已知GH//BC, , , 给出下列结论:①;②;③;④HE平分∠AHG;其中正确的有( )
A、小明说法正确,小亮说法错误 B、小明说法正确,小亮说法正确 C、小明说法错误,小亮说法正确 D、小明说法错误,小亮说法错误10. 如图,已知GH//BC, , , 给出下列结论:①;②;③;④HE平分∠AHG;其中正确的有( )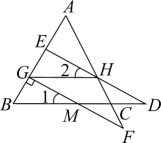 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、作图题(共8分)
-
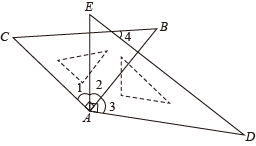
11. 如图, 内有一点 .
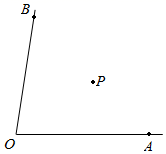 (1)、过点 画 交 于点 ,画 交 于点 ;(2)、图中不添加其它的字母,写出所有与 相等的角.
(1)、过点 画 交 于点 ,画 交 于点 ;(2)、图中不添加其它的字母,写出所有与 相等的角.三、解答题(共7题,共58分)
-
12. 如图, , . 求证: .

证明:∵( ),( ),
∴( ),∴( ),
∴( ),
∵( ),
∴( ),
∴( ).
13. 请将下列证明过程补充完整:已知:如图,点P在CD上,已知 , .

求证:
证明:∵(已知)
∴▲ // ▲ ( )
∴ ▲ ( )
又∵(已知)
∴ ▲
即 ▲ (等式的性质)
∴//(内错角相等,两直线平行)
∴( )
14. 如图,已知: , , 你能确定图中与的数量关系吗?请写出你的结论并进行证明. 15. 如图1,已知AB//CD,点G在上,点H在上,连接、 , , .
15. 如图1,已知AB//CD,点G在上,点H在上,连接、 , , . (1)、求证:AB//EF;(2)、如图2,若 , 延长交的延长线于点M,请直接写出图2中所有与互余的角.16. 如图:
(1)、求证:AB//EF;(2)、如图2,若 , 延长交的延长线于点M,请直接写出图2中所有与互余的角.16. 如图: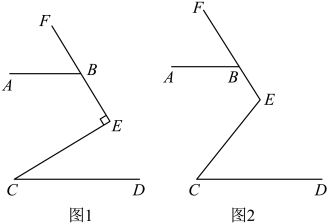 (1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:17. 如图,直线ABCD,直线与、分别交于点、 , 小安将一个含角的直角三角板按如图①放置,使点、分别在直线、上,且在点、的右侧, , .
(1)、如图1,∠CEF=90°,点B在射线EF上,若∠ABF=50°,∠C=40° ,试判断AB、CD的位置关系,并说明理由;(2)、如图2,∠CEF=120° ,点B在射线EF上,且 . 则∠ABE与∠C的数量关系为:17. 如图,直线ABCD,直线与、分别交于点、 , 小安将一个含角的直角三角板按如图①放置,使点、分别在直线、上,且在点、的右侧, , . (1)、填空:(填“”“”或“”);(2)、若的平分线交直线于点 , 如图②.
(1)、填空:(填“”“”或“”);(2)、若的平分线交直线于点 , 如图②.①当ONEF,PMEF时,求的度数;
②小安将三角板保持PMEF并向左平移,在平移的过程中求的度数(用含的式子表示).
18. 如图1,点E、F分别在直线AB、CD上,点P为AB、CD之间的一点,且 .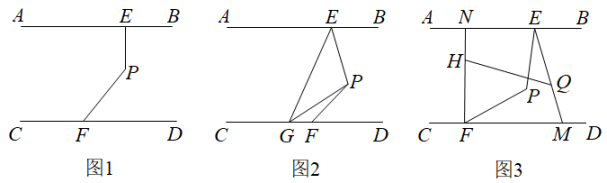 (1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.
(1)、求证:;(2)、如图2,点G在射线FC上,PG平分 , , 探究与之间的数量关系.并说明理由;(3)、如图3, , . 直线HQ分别交FN,EM于H、Q两点,若 , 求的度数.四、填空题(每题4分,共24分)
-
19. ∠α与∠β的两边分别平行,且∠α比∠β大30°,则∠α= .20. 一副直角三角板如图放置,点C在的延长线上, , , 则的度数为 .
 21. 如图 , AB与CE的关系是 , 此时若∠3=30°,则∠B=°.
21. 如图 , AB与CE的关系是 , 此时若∠3=30°,则∠B=°.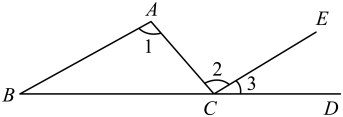
-