2023年浙教版数学七年级下册全方位训练卷1.2同位角、内错角、同旁内角
试卷更新日期:2023-01-12 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,图中的∠1与∠2是( ).
 A、对顶角 B、同位角 C、内错角 D、同旁内角2. 如图,则∠3的同旁内角是 ( )
A、对顶角 B、同位角 C、内错角 D、同旁内角2. 如图,则∠3的同旁内角是 ( )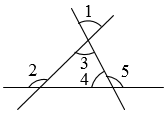 A、∠1 B、∠2 C、∠4 D、∠53. 如图所示,在所标识的角中,内错角是( )
A、∠1 B、∠2 C、∠4 D、∠53. 如图所示,在所标识的角中,内错角是( )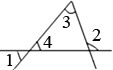 A、和 B、和 C、和 D、和4. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( )
A、和 B、和 C、和 D、和4. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( ) A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角5. 如图,下列说法错误的是( )
A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角5. 如图,下列说法错误的是( ) A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角6. 如图,直线和被直线所截,则( )
A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角6. 如图,直线和被直线所截,则( ) A、和是同位角 B、和是内错角 C、和是同位角 D、和是内错角7. 如图,按各组角的位置判断错误的是( )
A、和是同位角 B、和是内错角 C、和是同位角 D、和是内错角7. 如图,按各组角的位置判断错误的是( ) A、∠1与∠4是同旁内角 B、∠3与∠4是内错角 C、∠5与∠6是同旁内角 D、∠2与∠5是同位角8. 同学们可伤照图用双手表示“三线八角“困形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( )
A、∠1与∠4是同旁内角 B、∠3与∠4是内错角 C、∠5与∠6是同旁内角 D、∠2与∠5是同位角8. 同学们可伤照图用双手表示“三线八角“困形(两大拇指代表被截直线,食指代表截线).下面三幅图依次表示( ) A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角9. 如图, 和 属于同位角的有( )
A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角9. 如图, 和 属于同位角的有( )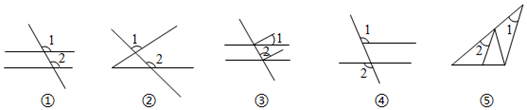 A、①②③ B、②③④ C、③④⑤ D、①②⑤10. 如图,与是( )形成的内错角
A、①②③ B、②③④ C、③④⑤ D、①②⑤10. 如图,与是( )形成的内错角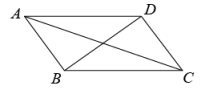 A、直线、被直线所截 B、直线、被直线所截 C、直线、被直线所截 D、直线、被直线所截
A、直线、被直线所截 B、直线、被直线所截 C、直线、被直线所截 D、直线、被直线所截二、填空题(第11题6分,12-17题每题3分,共24分)
-
11. 看图填空:
 (1)、∠1和∠4是角;(2)、∠1和∠3是角;(3)、∠2和∠D是角;(4)、∠3和∠D是角;(5)、∠4和∠D是角;(6)、∠4和∠B是角.12. 如图所标的5个角中,∠1与是同位角,∠5与是同旁内角.
(1)、∠1和∠4是角;(2)、∠1和∠3是角;(3)、∠2和∠D是角;(4)、∠3和∠D是角;(5)、∠4和∠D是角;(6)、∠4和∠B是角.12. 如图所标的5个角中,∠1与是同位角,∠5与是同旁内角. 13. 如图,与是直线和直线被直线所截形成的 .
13. 如图,与是直线和直线被直线所截形成的 . 14. 如图,若 , 被 所截,则 与是内错角.
14. 如图,若 , 被 所截,则 与是内错角. 15. 如图,直线和被第三条直线所截,与成内错角的是 .
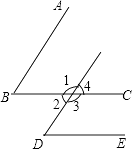
15. 如图,直线和被第三条直线所截,与成内错角的是 . 16. 如图,共有对同位角,有对内错角,有对同旁内角.
16. 如图,共有对同位角,有对内错角,有对同旁内角.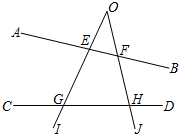 17. 如图,下列结论:①∠2与∠3是内错角;②∠1与∠A是同位角;③∠A与∠B是同旁内角;④∠B与∠ACB不是同旁内角,其中正确的是 .(只填序号)
17. 如图,下列结论:①∠2与∠3是内错角;②∠1与∠A是同位角;③∠A与∠B是同旁内角;④∠B与∠ACB不是同旁内角,其中正确的是 .(只填序号)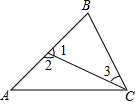
三、解答题(共8题,共66分)
-
18. 图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
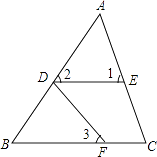 19. 如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角.
19. 如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角. 20. 如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?
20. 如图所示,∠1与∠2,∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角?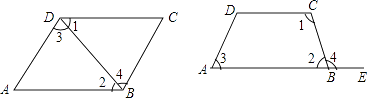 21. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
21. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想. (1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.22. 如图所示,回答下列问题.
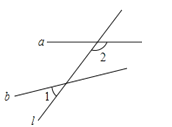
(1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.22. 如图所示,回答下列问题. (1)、请写出直线AB.CD被AC所截形成的内错角;(2)、请写出直线AB.CD被BE所截形成的同位角;(3)、找出图中∠1的所有同旁内角.23. 如图,直线a、b被直线l所截,已知∠1=40°,试求∠2的同位角及同旁内角的度数.
(1)、请写出直线AB.CD被AC所截形成的内错角;(2)、请写出直线AB.CD被BE所截形成的同位角;(3)、找出图中∠1的所有同旁内角.23. 如图,直线a、b被直线l所截,已知∠1=40°,试求∠2的同位角及同旁内角的度数.