2023年中考数学精选真题实战测试22 一次函数 B
试卷更新日期:2023-01-12 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 点在正比例函数()的图象上,则k的值为( )A、-15 B、15 C、 D、2. 如图,直线 分别与 轴、 轴交于点 和点 ,直线 分别与 轴、 轴交于点 和点 ,点 是 内部 (包括边上)的一点,则 的最大值与最小值之差为( )
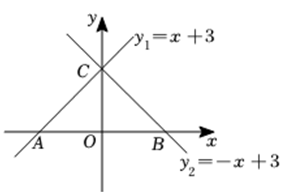 A、 B、 C、 D、3. 一辆汽车油箱中剩余的油量与已行驶的路程的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为时,那么该汽车已行驶的路程为( )
A、 B、 C、 D、3. 一辆汽车油箱中剩余的油量与已行驶的路程的对应关系如图所示,如果这辆汽车每千米的耗油量相同,当油箱中剩余的油量为时,那么该汽车已行驶的路程为( ) A、 B、 C、 D、4. 在一次函数中,y的值随x值的增大而增大,且 , 则点在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限5. 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A、 B、 C、 D、4. 在一次函数中,y的值随x值的增大而增大,且 , 则点在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限5. 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( ) A、x>3 B、x<3 C、x<1 D、x>16. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A、x>3 B、x<3 C、x<1 D、x>16. 小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )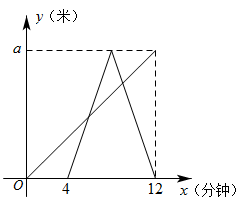 A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟7. 如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )
A、2.7分钟 B、2.8分钟 C、3分钟 D、3.2分钟7. 如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(10,4),四边形ABEF是菱形,且tan∠ABE=.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分,则直线l的解析式为( )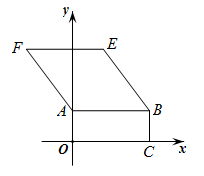 A、 B、 C、 D、8. 一次函数的值随的增大而增大,则点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 在同一平面直角坐标系中,一次函数与的图像可能是( )A、
A、 B、 C、 D、8. 一次函数的值随的增大而增大,则点所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 在同一平面直角坐标系中,一次函数与的图像可能是( )A、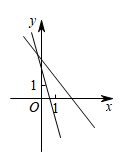 B、
B、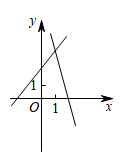 C、
C、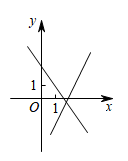 D、
D、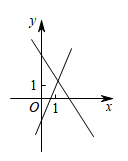 10. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论:
10. 在同一平面直角坐标系中,一次函数与的图象如图所示,小星根据图象得到如下结论: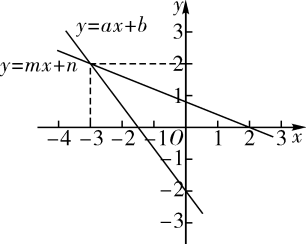
①在一次函数的图象中,的值随着值的增大而增大;②方程组的解为;③方程的解为;④当时,.
其中结论正确的个数是( )
A、1 B、2 C、3 D、4二、填空题(每空3分,共18分)
-
11. 已知直线y=kx+b过第一象限且函数值随着x的增大而减小,请列举出来这样的一条直线: .12. 将双曲线向右平移2个单位,再向下平移1个单位,得到的新双曲线与直线相交于2022个点,则这2022个点的横坐标之和为 .13. 如图,函数的图象经过点 , 则关于的不等式的解集为.
 14. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.
14. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.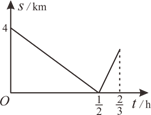 15. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .
15. 如图,已知反比例函数过A , B两点,A点坐标 ,直线 经过原点,将线段 绕点B顺时针旋转90°得到线段 ,则C点坐标为 .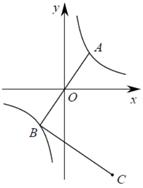 16. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.
16. 如图,是等边三角形,直线经过它们的顶点 , 点在x轴上,则点的横坐标是.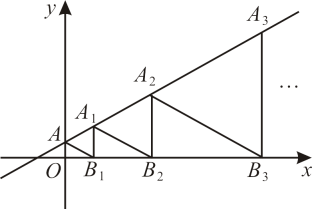
三、解答题(共8题,共72分)
-
17. 物理实验证实:在弹性限度内,某弹簧长度y( )与所挂物体质量x( )满足函数关系 .下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
x
0
2
5
y
15
19
25
(1)、求y与x的函数关系式;(2)、当弹簧长度为20 时,求所挂物体的质量.18. 在平面直角坐标系内有三点A(−1,4)、B(−3,2)、C(0,6).(1)、求过其中两点的直线的函数表达式(选一种情形作答);(2)、判断A、B、C三点是否在同一直线上,并说明理由.19. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快.在一段时间内,水温(℃)与加热时间之间近似满足一次函数关系,根据记录的数据,画函数图象如下: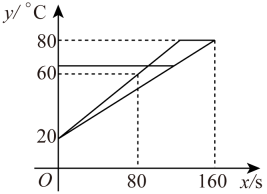 (1)、加热前水温是℃;(2)、求乙壶中水温关于加热时间的函数解析式;(3)、当甲壶中水温刚达到80℃时,乙壶中水温是℃.20. A,B两地相距 , 甲、乙两人分别开车从A地出发前往B地,其中甲先出发 , 如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题:
(1)、加热前水温是℃;(2)、求乙壶中水温关于加热时间的函数解析式;(3)、当甲壶中水温刚达到80℃时,乙壶中水温是℃.20. A,B两地相距 , 甲、乙两人分别开车从A地出发前往B地,其中甲先出发 , 如图是甲,乙行驶路程随行驶时间变化的图象,请结合图象信息.解答下列问题: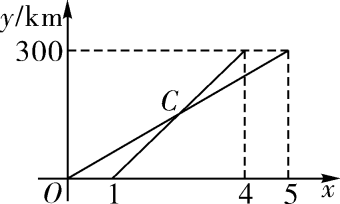 (1)、填空:甲的速度为;(2)、分别求出与x之间的函数解析式;(3)、求出点C的坐标,并写点C的实际意义.21. 某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量 (件)与销售时间 (天)之间的关系式是 ,销售单价 (元/件)与销售时间 (天)之间的函数关系如图所示.
(1)、填空:甲的速度为;(2)、分别求出与x之间的函数解析式;(3)、求出点C的坐标,并写点C的实际意义.21. 某商户购进一批童装,40天销售完毕.根据所记录的数据发现,日销售量 (件)与销售时间 (天)之间的关系式是 ,销售单价 (元/件)与销售时间 (天)之间的函数关系如图所示.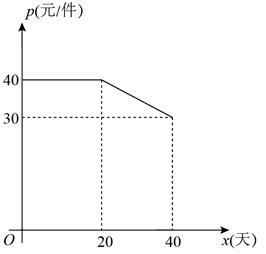 (1)、第15天的日销售量为件;(2)、当 时,求日销售额的最大值;(3)、在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?22. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:
(1)、第15天的日销售量为件;(2)、当 时,求日销售额的最大值;(3)、在销售过程中,若日销售量不低于48件的时间段为“火热销售期”,则“火热销售期”共有多少天?22. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个商店的优惠活动如下:甲:所有商品按原价8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
设需要购买体育用品的原价总额为元,去甲商店购买实付元,去乙商店购买实付元,其函数图象如图所示.
 (1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.23. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.
(1)、分别求 , 关于的函数关系式;(2)、两图象交于点 , 求点坐标;(3)、请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.23. 某校组织学生从学校出发,乘坐大巴前往基地进行研学活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知大巴行驶的速度是40千米/小时,轿车行驶的速度是60千米/小时.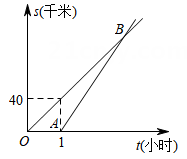 (1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.24. 如图,平面直角坐标系中,线段AB的端点为 , .
(1)、求轿车出发后多少小时追上大巴?此时,两车与学校相距多少千米?(2)、如图,图中OB,AB分别表示大巴、轿车离开学校的路程s(千米)与大巴行驶的时间t(小时)的函数关系的图象.试求点B的坐标和AB所在直线的解析式;(3)、假设大巴出发a小时后轿车出发追赶,轿车行驶了1.5小时追上大巴,求a的值.24. 如图,平面直角坐标系中,线段AB的端点为 , .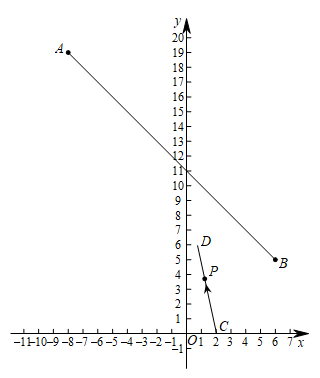 (1)、求AB所在直线的解析式;(2)、某同学设计了一个动画:在函数 中,分别输入m和n的值,使得到射线CD , 其中 .当c=2时,会从C处弹出一个光点P , 并沿CD飞行;当 时,只发出射线而无光点弹出.
(1)、求AB所在直线的解析式;(2)、某同学设计了一个动画:在函数 中,分别输入m和n的值,使得到射线CD , 其中 .当c=2时,会从C处弹出一个光点P , 并沿CD飞行;当 时,只发出射线而无光点弹出.①若有光点P弹出,试推算m , n应满足的数量关系;
②当有光点P弹出,并击中线段AB上的整点(横、纵坐标都是整数)时,线段AB就会发光,求此时整数m的个数.