2023年中考数学精选真题实战测试21 一次函数 A
试卷更新日期:2023-01-12 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、2. 在平面直角坐标系中,将函数y=3x +2的图象向下平移3个单位长度,所得的函数的解析式是( )A、y=3x+5 B、y=3x﹣5 C、y=3x+1 D、y=3x﹣13. 在同一平面直角坐标系中,函数y=ax+b与(其中a,b是常数,ab≠0)的大致图象是( )A、
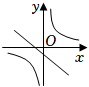 B、
B、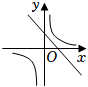 C、
C、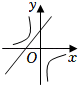 D、
D、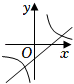 4. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )
4. 在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 将绕点逆时针旋转到如图的位置,的对应点恰好落在直线上,连接 , 则的长度为( )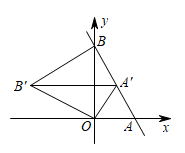 A、 B、 C、2 D、5. 根据图像,可得关于x的不等式的解集是( )
A、 B、 C、2 D、5. 根据图像,可得关于x的不等式的解集是( )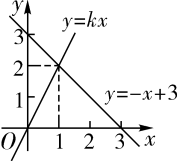 A、 B、 C、 D、6. 汽车油箱中有汽油 , 如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为 . 当时,y与x的函数解析式是( )A、 B、 C、 D、7. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A、 B、 C、 D、6. 汽车油箱中有汽油 , 如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:)的增加而减少,平均耗油量为 . 当时,y与x的函数解析式是( )A、 B、 C、 D、7. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )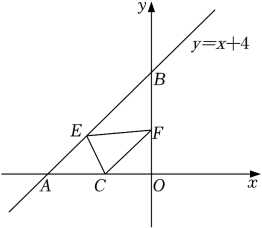 A、 , B、 , C、 , D、 ,8. 图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强p(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为 , 其图象如图2所示,其中为青海湖水面大气压强,k为常数且.根据图中信息分析(结果保留一位小数),下列结论正确的是( )
A、 , B、 , C、 , D、 ,8. 图1是我国青海湖最深处的某一截面图,青海湖水面下任意一点A的压强p(单位:cmHg)与其离水面的深度h(单位:m)的函数解析式为 , 其图象如图2所示,其中为青海湖水面大气压强,k为常数且.根据图中信息分析(结果保留一位小数),下列结论正确的是( )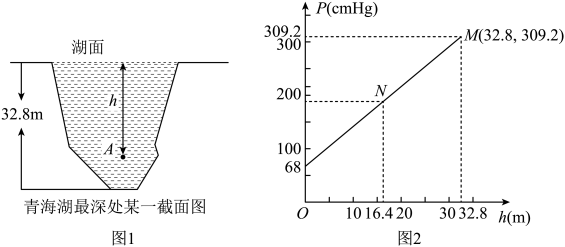 A、青海湖水深16.4m处的压强为188.6cmHg B、青海湖水面大气压强为76.0cmHg C、函数解析式中自变量h的取值范围是 D、P与h的函数解析式为9. 若一次函数的函数值y随x的增大而减小,则k值可能是( )A、2 B、 C、 D、10. 如图,在平面直角坐标系中,直线 与直线 相交于点A,则关于x,y的二元一次方程组 的解是( )
A、青海湖水深16.4m处的压强为188.6cmHg B、青海湖水面大气压强为76.0cmHg C、函数解析式中自变量h的取值范围是 D、P与h的函数解析式为9. 若一次函数的函数值y随x的增大而减小,则k值可能是( )A、2 B、 C、 D、10. 如图,在平面直角坐标系中,直线 与直线 相交于点A,则关于x,y的二元一次方程组 的解是( )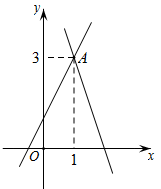 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
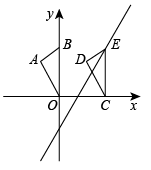
11. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
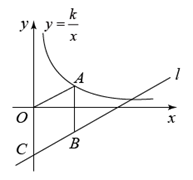
 12. 点在一次函数的图像上,当时, , 则a的取值范围是 .13. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:
12. 点在一次函数的图像上,当时, , 则a的取值范围是 .13. 如图,点A在双曲线 上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:① ②当 时, ③ ④
则所有正确结论的序号是 .
 14. 甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图象经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是.15. 如图,已知点 , ,直线 经过点 .试探究:直线与线段 有交点时 的变化情况,猜想 的取值范围是.
14. 甲、乙两位同学各给出某函数的一个特征,甲:“函数值y随自变量x增大而减小”;乙:“函数图象经过点(0,2)”,请你写出一个同时满足这两个特征的函数,其表达式是.15. 如图,已知点 , ,直线 经过点 .试探究:直线与线段 有交点时 的变化情况,猜想 的取值范围是.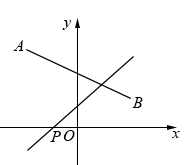 16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .
16. 如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 .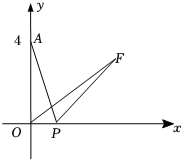
三、解答题(共8题,共72分)
-
17. 小丽从甲地匀速步行去乙地,小华骑自行车从乙地匀速前往甲地,同时出发,两人离甲地的距离(m)与出发时间(min)之间的函数关系如图所示.
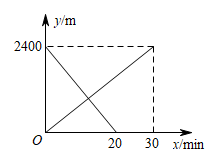 (1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.18. 如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.
(1)、小丽步行的速度为m/min;(2)、当两人相遇时,求他们到甲地的距离.18. 如图,直线y=x+1与x轴交于点A,点A关于y轴的对称点为A′,经过点A′和y轴上的点B(0,2)的直线设为y=kx+b.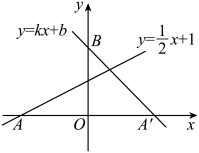 (1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.19. 在平面直角坐标系中,函数的图象经过点 , , 且与轴交于点 .(1)、求该函数的解析式及点的坐标;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.20. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
(1)、求点A′的坐标;(2)、确定直线A′B对应的函数表达式.19. 在平面直角坐标系中,函数的图象经过点 , , 且与轴交于点 .(1)、求该函数的解析式及点的坐标;(2)、当时,对于的每一个值,函数的值大于函数的值,直接写出的取值范围.20. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
 (1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?21. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.
(1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?21. 某水果店购进甲、乙两种苹果的进价分别为8元/、12元/ , 这两种苹果的销售额y(单位:元)与销售量x(单位:)之间的关系如图所示.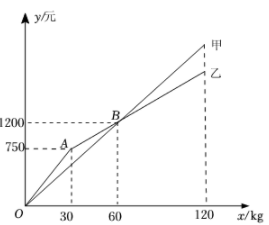 (1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.22. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下
(1)、写出图中点B表示的实际意义;(2)、分别求甲、乙两种苹果销售额y(单位:元)与销售量x(单位:)之间的函数解析式,并写出x的取值范围;(3)、若不计损耗等因素,当甲、乙两种苹果的销售量均为时,它们的利润和为1500元.求a的值.22. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单长度后得到的点Q' 也在G上时,求G在≤≤的图象的最高点的坐标.
23. 如图,在平面直角坐标系中,一次函数的图象与x轴交于点A,与y轴交于点 , 与直线OC交于点 . (1)、求直线AB的函数表达式;(2)、过点C作轴于点D,将沿射线CB平移得到的三角形记为 , 点A,C,D的对应点分别为 , , , 若与重叠部分的面积为S,平移的距离 , 当点与点B重合时停止运动.
(1)、求直线AB的函数表达式;(2)、过点C作轴于点D,将沿射线CB平移得到的三角形记为 , 点A,C,D的对应点分别为 , , , 若与重叠部分的面积为S,平移的距离 , 当点与点B重合时停止运动.①若直线交直线OC于点E,则线段的长为(用含有m的代数式表示);
②当时,S与m的关系式为;
③当时,m的值为 .
24. 定义:对于一次函数 ,我们称函数为函数的“组合函数”.(1)、若m=3,n=1,试判断函数是否为函数的“组合函数”,并说明理由;(2)、设函数与的图象相交于点P.①若 , 点P在函数的“组合函数”图象的上方,求p的取值范围;
②若p≠1,函数的“组合函数”图象经过点P.是否存在大小确定的m值,对于不等于1的任意实数p,都有“组合函数”图象与x轴交点Q的位置不变?若存在,请求出m的值及此时点Q的坐标;若不存在,请说明理由.