初中数学同步训练必刷题(人教版七年级下册 5.3.1平行线的性质)
试卷更新日期:2023-01-12 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,直线// , 则的度数是( )
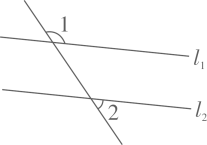 A、30° B、40° C、50° D、65°2. 如图,直线 , 直线 , 若 , 则的度数为( )
A、30° B、40° C、50° D、65°2. 如图,直线 , 直线 , 若 , 则的度数为( ) A、50° B、45° C、40° D、30°3. 如图,在四边形中,下列结论正确的是( )
A、50° B、45° C、40° D、30°3. 如图,在四边形中,下列结论正确的是( ) A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图所示, , , 若 , 则的度数为( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则4. 如图所示, , , 若 , 则的度数为( ) A、100° B、110° C、120° D、130°5. 如图,将一副三角板的直角顶点重合,且使 , 则的度数是( )
A、100° B、110° C、120° D、130°5. 如图,将一副三角板的直角顶点重合,且使 , 则的度数是( )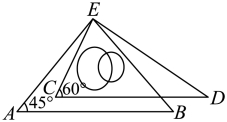 A、 B、 C、 D、6. 如图,已知直线 , 点B在直线a上,点A,C在直线b上,且 . 若 , 则∠2的度数是( )
A、 B、 C、 D、6. 如图,已知直线 , 点B在直线a上,点A,C在直线b上,且 . 若 , 则∠2的度数是( )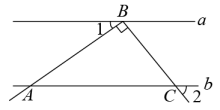 A、45° B、50° C、55° D、60°7. 如图,直线 , 直线与直线 , 分别交于点 , 点 , 于点 , 交直线于点 . 如果 , 那么的度数为( )
A、45° B、50° C、55° D、60°7. 如图,直线 , 直线与直线 , 分别交于点 , 点 , 于点 , 交直线于点 . 如果 , 那么的度数为( )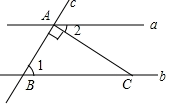 A、 B、 C、 D、8. 如图,直线AB∥CD,∠EFB=60°,则∠CGE的度数是( )
A、 B、 C、 D、8. 如图,直线AB∥CD,∠EFB=60°,则∠CGE的度数是( )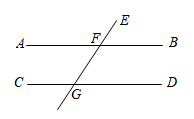 A、130° B、110° C、120° D、60°9. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( )
A、130° B、110° C、120° D、60°9. 如图,弯形管道ABCD的拐角∠ABC=120°,要保证管道 , 则∠BCD等于( ) A、60° B、50° C、70° D、65°10. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( )
A、60° B、50° C、70° D、65°10. 如图, , 平分 , 且 , 垂足为 , 则与的数量关系是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共24分)
-
11. 如图,已知直线、被直线所截,且∥ , ∠1=°,那么∠2 =度;
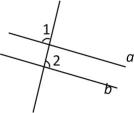 12. 已知:如图,在中, , 过点且平行于 , 若 , 则的度数为 .
12. 已知:如图,在中, , 过点且平行于 , 若 , 则的度数为 . 13. 如图,已知直线ab,cd,若∠1、∠2是图中的两个角,且这两个角的两边分别平行, , , 则x值为 .
13. 如图,已知直线ab,cd,若∠1、∠2是图中的两个角,且这两个角的两边分别平行, , , 则x值为 . 14. 如图,将一块含有角的直角三角板的两个顶点放在作业本两行线上.如果 , 那么的度数是 .
14. 如图,将一块含有角的直角三角板的两个顶点放在作业本两行线上.如果 , 那么的度数是 . 15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若 , , 则的度数为 .
15. 已知:如图,点D是射线AB上一动点,连接CD,过点D作交直线AC于点E,若 , , 则的度数为 . 16. 如图,已知AB∥CD,BC∥DE,那么∠B +∠D =.
16. 如图,已知AB∥CD,BC∥DE,那么∠B +∠D =.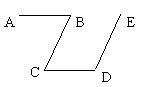 17. 如图,直线a与∠AOB的一边射线OA相交,∠1=130°,向下平移直线a得到直线b,与∠AOB的另一边射线OB相交,则∠2+∠3= .
17. 如图,直线a与∠AOB的一边射线OA相交,∠1=130°,向下平移直线a得到直线b,与∠AOB的另一边射线OB相交,则∠2+∠3= .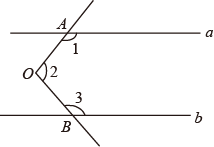 18. 如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=°.
18. 如图,AB∥CD,AD⊥AC,∠BAD=35°,则∠ACD=°.
三、解答题(共8题,共66分)
-
19. 请将下列证明过程补充完整:
已知:如图,点P在CD上,已知 , .

求证:
证明:∵(已知)
∴▲ // ▲ ( )
∴ ▲ ( )
又∵(已知)
∴ ▲
即 ▲ (等式的性质)
∴//(内错角相等,两直线平行)
∴( )
20. 如图,// , , EF平分 , , 垂足为点H,求的度数. 21. 如图,四边形ABCD中ABCD,在BC的延长线上取一点E,连接AE交CD于点F,且满足 , . 求证:ADBE
21. 如图,四边形ABCD中ABCD,在BC的延长线上取一点E,连接AE交CD于点F,且满足 , . 求证:ADBE 22. 如图, , , ,求 、 的度数.
22. 如图, , , ,求 、 的度数.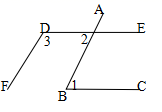 23. 如图,已知 ,∠ ,求 、 、 的度数.
23. 如图,已知 ,∠ ,求 、 、 的度数. 24. 如图,在△ABC中, , ,
24. 如图,在△ABC中, , , (1)、求证:;(2)、若DG平分∠ADC, , 求∠EFC的度数.25. 如图,已知AB∥CD,EF∥MN,∠1=115°,
(1)、求证:;(2)、若DG平分∠ADC, , 求∠EFC的度数.25. 如图,已知AB∥CD,EF∥MN,∠1=115°, (1)、求∠2和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.26. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.
(1)、求∠2和∠4的度数;(2)、本题隐含着一个规律,请你根据(1)的结果进行归纳:如果一个角的两边分别平行于另一个角的两边,那么这两个角;(3)、利用(2)的结论解答:如果两个角的两边分别平行,其中一个角是另一个角的两倍,求这两个角的大小.26. 在一次数学综合实践活动课上,同学们进行了如下探究活动:将一块等腰直角三角板的顶点G放置在直线上,旋转三角板.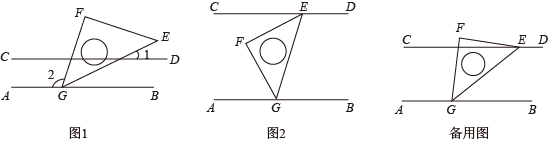 (1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.
(1)、如图1,在边上任取一点P(不同于点G,E),过点P作 , 若 , 求的度数;(2)、如图2,过点E作 , 请探索并说明与之间的数量关系;(3)、将三角板绕顶点G转动,过点E作 , 并保持点E在直线的上方.在旋转过程中,探索与之间的数量关系,并说明理由.