（华师大版）2022-2023学年八年级数学下册16.2 分式的运算同步测试

试卷更新日期：2023-01-12 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，设 $k = \frac{乙图中阴影部分面积}{甲图中阴影部分面积}$ （ $a > b > 0$ ），则k的值可以为（）

A、 $\frac{3}{5}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析
2. 计算 $\frac{1}{a} \div a$ 的结果为（）

A、a B、 $\frac{1}{a^{2}}$ C、1 D、 $a^{2}$

查看试题解析
3. 有甲，乙两块边长为a米（a>8）的正方形试验田．负责试验田的杨师傅将试验田的形状进行了调整（如图）：沿甲试验田的一边在试验田内修了1米宽的水池，又在邻边增加了1米宽的田地；沿乙试验田的一组邻边在试验田内均修了1米宽的小路．杨师傅在调整后的试验田上种植了某种小麦，其中甲试验田收获了200千克小麦，乙试验田收获了150千克小麦，对于这两块试验田的单位面积产量，下列说法正确的是（）

A、甲试验田的单位面积产量高 B、乙试验田的单位面积产量高 C、两块试验田的单位面积产量一样 D、无法判断哪块试验田的单位面积产量高

查看试题解析
4. 化简 $\frac{2}{x^{2} - 1} \div \frac{1}{x - a}$ 的结果是 $\frac{2}{x - 1}$ ，则 $a$ 的值是（）

A、1 B、-1 C、2 D、-2

查看试题解析
5. 下列运算正确的是（）

A、 $2 a^{- 3} \cdot a^{4} = 2 a^{- 12}$ B、 ${(- 3 a^{2})}^{3} = - 9 a^{6}$ C、 $a^{2} \div a \times \frac{1}{a} = a^{2}$ D、 $a \cdot a^{3} + a^{2} \cdot a^{2} = 2 a^{4}$

查看试题解析
6. 下列各式中，计算结果正确的有（）
⑴ $\frac{3 x}{x^{2}} \cdot \frac{x}{3 x} = \frac{1}{x}$ （2） $a \div b \times \frac{1}{b} = a$ （3） $\frac{a}{a^{2} - 1} \div \frac{a^{2}}{a^{2} + a} = \frac{1}{a - 1}$ （4） $8 a^{2} b^{2} \div (- \frac{3 a}{4 b^{2}}) = - 6 a^{3} b$ ⑸ $\frac{1}{c} + \frac{2}{c} = \frac{3}{c}$ （6） $\frac{0.2 a + b}{0.7 a - b} = \frac{2 a + b}{7 a - b}$

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若 $x y = - 6$ ，其中 $x > y$ ，则下列分式的值一定比 $\frac{y}{x}$ 的值大的是（）

A、 $\frac{3 y}{3 x}$ B、 $\frac{3 y}{x}$ C、 $- \frac{3}{x}$ D、 $\frac{y + 3}{x}$

查看试题解析
8. 已知 $\frac{1}{x} - \frac{1}{y} = 3$ ，则分式 $\frac{5 x + x y - 5 y}{x - x y - y}$ 的值为（）

A、8 B、 $\frac{7}{2}$ C、 $\frac{2}{7}$ D、4

查看试题解析
9. 照相机成像应用了一个重要原理，用公式 $\frac{1}{f} = \frac{1}{u} + \frac{1}{v} (v \neq f)$ 表示，其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离．已知f，v，则u＝（）

A、 $\frac{f v}{f - v}$ B、 $\frac{f - v}{f v}$ C、 $\frac{f v}{v - f}$ D、 $\frac{v - f}{f v}$

查看试题解析
10. 如果 $x > y > 1$ ，那么 $\frac{y - 1}{x - 1} - \frac{y}{x}$ 的值是（）

A、正数 B、负数 C、零 D、不确定

查看试题解析

二、填空题

11. 计算 $\frac{x^{2} - 4}{x} \cdot \frac{6 x^{2}}{4 - 2 x}$ 的结果是．

查看试题解析
12. 甲、乙两个工程队合修一条公路，已知甲工程队每天修 $(a^{2} - 4)$ 米，乙工程队每天修 ${(a - 2)}^{2}$ 米（其中 $a > 2$ ），则甲工程队修900米所用时间与乙工程队修600米所用时间的比值是．（用含a的式子表示）

查看试题解析
13. 某药品原来每盒p元，现在每盒提高3元，用200元买这种药品现在比原来少买盒．

查看试题解析
14. 计算 $\frac{1}{x - 1} - \frac{1}{x (x - 1)}$ 的结果为．

查看试题解析
15. 某种弹簧秤原来的长度为l，悬挂重物后的长度L可以用公式 $L = l + \frac{m}{k}$ 表示，其中m是悬挂物的质量，k是常数，则m= ．（用 $L ， l ， k$ 表示）

查看试题解析

三、解答题

16. （Ⅰ）计算：（a﹣b）（a²+ab+b²）
（Ⅱ）利用所学知识以及（Ⅰ）所得等式，化简代数式 $\frac{m^{3} - n^{3}}{m^{2} + m n + n^{2}}$ ÷ $\frac{m^{2} - n^{2}}{m^{2} + 2 m n + n^{2}}$ ．

查看试题解析
17. 下面是小明计算 $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ÷ $\frac{a + 1}{a - 1}$ · $\frac{1 - a}{1 + a}$ 的过程:
解: $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ÷ $\frac{a + 1}{a - 1}$ · $\frac{1 - a}{1 + a}$
= $\frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ÷(-1)   第一步
= $\frac{(1 - a) (1 + a)}{{(a - 1)}^{2}}$    第二步
= $\frac{1 + a}{1 - a}$ .   第三步
上述过程是否有错,若有错,是从第几步开始出错的?并写出正确的计算过程.

查看试题解析
18. 先化简 $(\frac{1}{x^{2}} - \frac{1}{y^{2}}) \div {(\frac{1}{x} + \frac{1}{y})}^{2}$ ，然后从 $0 < y < x \leq 3$ 的范围内选择一组合适的整数作为 $x ， y$ 的值代入求值．

查看试题解析

四、综合题

19. 运算律是解决许多数学问题的基础，在运算中有重要的作用，充分运用运算律能使计算简便高效.
例如： $(- 125 \frac{5}{7}) ÷ (- 5)$ .

解： $(- 125 \frac{5}{7}) \div (- 5) = 125 \frac{5}{7} \times \frac{1}{5} = (125 + \frac{5}{7}) \times \frac{1}{5} = 125 \times \frac{1}{5} + \frac{5}{7} \times \frac{1}{5} = 25 + \frac{1}{7} = 25 \frac{1}{7}$ .

(1)、计算： $(- \frac{3}{2} - \frac{2}{3}) \div \frac{1}{6}$ ， A同学的计算过程如下：
原式 $= (- \frac{3}{2} - \frac{2}{3}) \times 6 = (- \frac{3}{2}) \times 6 + \frac{2}{3} \times 6 = - 9 + 4 = - 5$ .
请你判断A同学的计算过程是否正确，若不正确，请你写出正确的计算过程.

(2)、请你参考例题，用运算律简便计算（请写出具体的解题过程）： $999 \times 118 \frac{4}{5} + 333 \times (- \frac{3}{5}) - 999 \times 118 \frac{3}{5}$ .

查看试题解析
20. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简.过程如图所示：

(1)、接力中，自己负责的一步出现错误的是

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

(2)、请你书写正确的化简过程，并在“1，0，2，﹣2”中选择一个合适的数求值.

查看试题解析
21. 老师在黑板上写了一个代数式的正确计算结果，随后用“黑板擦”遮住原代数式的一部分，如图.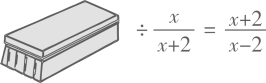

(1)、求被“黑板擦”遮住部分的代数式；

(2)、 $\frac{x + 2}{x - 2}$ 的值能等于0吗?请说明理由.

查看试题解析
22.

(1)、求当 $a = \sqrt{3}$ ， $b = - 1$ 时代数式 $- 2 a^{2} b - a + 3 b a + a^{2}$ 的值.

(2)、已知 $\frac{a + b}{a - b} = 7$ ，求 $\frac{2 (a + b)}{a - b} - \frac{a - b}{3 (a + b)}$ 的值.

查看试题解析
23. 在分式中，对于只含一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”，例如： $\frac{x + 1}{x - 1}$ ， $\frac{x^{2}}{x + 1}$ 这样的分式就是假分式；当分子的次数小于分母的次数时，我们称之为“真分式”，例如 $\frac{3}{x - 1}$ ， $\frac{- 3 x}{x^{2} + 1}$ 这样的分式就是真分式.我们知道，假分数可以化为带分数，类似地，假分式也可以化为“带分式”（即整式与真分式的和的形式），例如：
$\frac{x + 1}{x - 1}$ ＝ $\frac{(x - 1) + 2}{x - 1}$ ＝1+ $\frac{2}{x - 1}$ ， $\frac{x^{2}}{x + 1}$ ＝ $\frac{x^{2} - 1 + 1}{x + 1}$ ＝ $\frac{(x - 1) (x + 1) + 1}{x + 1}$ ＝x﹣1+ $\frac{1}{x + 1}$ .
参考上面的方法解决下列问题：

(1)、将分式 $\frac{x + 6}{x + 2}$ 化为带分式；

(2)、求分式 $\frac{23 - 9 n}{8 - n}$ 的最大值；（其中n为正整数）

(3)、已知分式 $\frac{2 t + 3}{t + 2}$ 的值是整数，求t的整数值.

查看试题解析

（华师大版）2022-2023学年八年级数学下册16.2 分式的运算 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（华师大版）2022-2023学年八年级数学下册16.2 分式的运算同步测试