人教版九年级数学2023年寒假专项训练----预习部分反比例函数的实际运用

试卷更新日期：2023-01-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 某电子商城推出分期付款购买电脑的活动，一台电脑的售价为1.2万元，前期付款4000元，后期每个月分期付一定的数额，则每个月的付款额 $y$ (元)与付款月数 $x$ 之间的函数关系式是（）

A、 $y = \frac{8000}{x}$ （x为正整数) B、 $y = \frac{8}{x}$ C、 $y = \frac{8000}{x}$ D、 $y = 8000 x$

查看试题解析
2. 研究发现，近视镜的度数y（度）与镜片焦距x（米）成反比例函数关系，小明佩戴的400度近视镜片的焦距为0.25米，经过一段时间的矫正治疗加之注意用眼健康，现在镜片焦距为0.4米，则小明的近视镜度数可以调整为（　　）

A、300度 B、500度 C、250度 D、200度

查看试题解析
3. 某工厂现有原材料100吨，每天平均用去x吨，这批原材料能用y天，则y与x之间的函数表达式为（）

A、 $y = 100 x$ B、 $y = \frac{100}{x}$ C、 $y = \frac{x}{2} + 100$ D、 $y = 100 - x$

查看试题解析
4. 地球周围的大气层阻挡了紫外线和宇宙射线对地球生命的伤害，同时产生一定的大气压，海拔不同，大气压不同，观察图中数据，你发现，正确的是（）

A、海拔越高，大气压越大 B、图中曲线是反比例函数的图象 C、海拔为4千米时，大气压约为70千帕 D、图中曲线表达了大气压和海拔两个量之间的变化关系

查看试题解析
5. 呼气式酒精测试仪中装有酒精气体传感器，可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻（图1中的 $R_{1}$ ）， $R_{1}$ 的阻值随呼气酒精浓度K的变化而变化（如图2），血液酒精浓度M与呼气酒精浓度K的关系见图3.下列说法不正确的是（）

A、呼气酒精浓度K越大， $R_{1}$ 的阻值越小 B、当K＝0时， $R_{1}$ 的阻值为100 C、当K＝10时，该驾驶员为非酒驾状态 D、当 $R_{1} = 20$ 时，该驾驶员为醉驾状态

查看试题解析
6. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压 $P$ （单位：千帕）随气球内气体的体积 $V$ （单位：立方米）的变化而变化， $P$ 随 $V$ 的变化情况如下表所示，那么在这个温度下，气球内气体的气压P与气球内气体的体积 $V$ 的函数关系最可能是
$V$ （单位：立方米）
64
48
38.4
32
24
…
$P$ （单位：千帕）
1.5
2
2.5
3
4
…

A、正比例函数 B、一次函数 C、二次函数 D、反比例函数

查看试题解析
7. 学校的自动饮水机，开机加热时每分钟上升10℃，加热到100℃，停止加热，水温开始下降.此时水温 $y$ （℃）与通电时间 $x (m i n)$ 成反比例关系.当水温将至20℃时，饮水机再自动加热，若水温在20℃时接通电源，水温y与通电时间x之间的关系如图所示，则下列说法中正确的是（）

A、水温从20℃加热到100℃，需要 $7 m i n$ B、水温下降过程中，y与x的函数关系式是 $y = \frac{400}{x}$ C、上午8点接通电源，可以保证当天9：30能喝到不超过40℃的水 D、水温不低于30℃的时间为 $\frac{77}{3} m i n$

查看试题解析

二、填空题

8. 科技小组为了验证某电路的电压U（V）、电流I（A）、电阻 $R (Ω)$ 三者之间的关系： $I = \frac{U}{R}$ ，测得数据如下：

$R (Ω)$

100

200

220

400

$I (A)$

2.2

1.1

1

0.55

那么，当电阻 $R = 55 Ω$ 时，电流 $I =$ A.

查看试题解析
9. 有一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度 $ρ (kg / m^{3})$ 是体积 $V (m^{3})$ 的反比例函数，它的图象如图，当 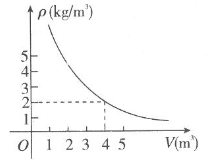$V = 2 m^{3}$ 时，气体的密度是 $kg / m^{3}$ .

查看试题解析
10. 某商场出倠一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价 $x$ (元)与日销售量 $y$ (个)之间有如下关系：

日销售单价x(元）

3

4

5

6

日销售量y(个）

20

15

12

10

则 $y$ 与 $x$ 之间的函数关系式为.

查看试题解析
11. 如图，矩形ABCD的顶点A、B分别在反比例函数 $y = \frac{4}{x} (x > 0)$ 与 $y = - \frac{2}{x} (x < 0)$ 的图象上，点C、D在x轴上，AB、BD分别交y轴于点E、F，则阴影部分的面积为．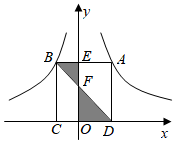

查看试题解析

三、解答题

12. 如图，一块砖的A，B，C三个面的面积比是 $4 ： 2 ： 1$ .如果B面向下放在地上，地面所受压强为 $a$ $P a$ ，那么A面和C面分别向下放在地上时，地面所受压强各是多少？

查看试题解析
13. 已知近视眼镜的度数y（度）与镜片焦距x（米）成反比例关系，且400度近视眼镜镜片的焦距为0.25米．小慧原来戴400度的近视眼镜，经过一段时间的矫正治疗后，现在只需戴镜片焦距为0.4米的眼镜了，求小慧所戴眼镜的度数降低了多少度．

查看试题解析

四、综合题

14. 在某一电路中，保持电压U不变，电流I（单位：A）与电阻R（单位： $Ω$ ）成反比例关系，当电阻 $R = 5 Ω$ 时，电流 $I = 2 A$ ．

(1)、求I与R之间的函数关系式；

(2)、当电流 $I = 0.5 A$ 时，求电阻R的值．

查看试题解析
15. 某蔬菜生产基地在气温较低时用装有恒温系统的大棚栽培一种在自然光照且温度为 $18 ℃$ 的条件下生长最快的新品种.下图是某天恒温系统从开启到关闭及关闭后大棚内的温度 $y (℃)$ 随时间 $x$ （小时）变化的函数图象，其中 $B C$ 段是双曲线 $y = \frac{k}{x}$ 的一部分.请根据图中信息解答下列问题：

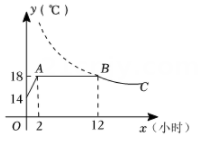(1)、恒温系统在这天保持大棚内的温度 $18 ℃$ 的时间有小时；

(2)、 $k =$ ；

(3)、当棚内温度不低于 $16 ℃$ 时，该蔬菜能够快速生长，则这天该蔬菜能够快速生长小时.

查看试题解析
16. 密闭容器内有一定质量的二氧化碳，当容器的体积V（单位： $m^{3}$ ）变化时，气体的密度 $ρ$ （单位： $k g / m^{}$ ）随之变化．已知密度 $ρ$ 与体积V是反比例函数关系，它的图象如图所示，当 $V = 5 m^{3}$ 时， $ρ = 1.98 k g / m^{3}$ ．

(1)、求密度 $ρ$ 关于体积V的函数解析式；

(2)、若 $3 \leq V \leq 9$ ，求二氧化碳密度 $ρ$ 的变化范围．

查看试题解析

$V$ （单位：立方米）	64	48	38.4	32	24	…
$P$ （单位：千帕）	1.5	2	2.5	3	4	…

$R (Ω)$	100	200	220	400
$I (A)$	2.2	1.1	1	0.55

日销售单价x(元）	3	4	5	6
日销售量y(个）	20	15	12	10

人教版九年级数学2023年寒假专项训练----预习部分 反比例函数的实际运用

一、单选题

二、填空题

三、解答题

四、综合题

人教版九年级数学2023年寒假专项训练----预习部分反比例函数的实际运用