（华师大版）2022-2023学年八年级数学下册16.1 分式及其基本性质同步测试

试卷更新日期：2023-01-12 类型：同步测试

进入出卷网下载

一、单选题

1. 使分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，这时x应为（）

A、x＝±1 B、x＝1 C、x＝1 且 x≠﹣1 D、x 的值不确定

查看试题解析
2. 若分式 $\frac{x}{| x | - 1}$ 无意义，则x的值是（）

A、0 B、1 C、-1 D、 $± 1$

查看试题解析
3. 下列式子是分式的是（）

A、x B、 $\frac{3}{x}$ C、 $\frac{4}{5}$ D、 $x^{2} y$

查看试题解析
4. 分式 $\frac{m + 3}{m - 3}$ 有意义的条件是（）

A、m≠3 B、m≠﹣3 C、m＝3 D、m＝﹣3

查看试题解析
5. 要使分式 $\frac{x + 2}{x + 1}$ 有意义，x的取值应满足（）

A、 $x \neq - 1$ B、 $x \neq - 1$ 且 $x \neq - 2$ C、 $x \neq - 2$ D、 $x = - 1$

查看试题解析
6. 把分式 $\frac{x^{2}}{2 x + y}$ 中的 $x$ 和 $y$ 都扩大2倍，分式的值（）

A、不变 B、扩大2倍 C、缩小2倍 D、扩大4倍

查看试题解析
7. 下列分式中，最简分式是（）

A、 $\frac{4}{2 x}$ B、 $\frac{x - 1}{x^{2} - 1}$ C、 $\frac{1}{x + 1}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
8. 化简 $\frac{a^{2} + a}{a^{2} - 1}$ 的结果是（）

A、 $\frac{a + 1}{a - 1}$ B、 $\frac{a}{a + 1}$ C、 $\frac{a}{a - 1}$ D、 $a + 1$

查看试题解析
9. 下列各式从左到右的变形一定正确的是（）

A、 $\frac{b}{a} = \frac{b + 1}{a + 1}$ B、 $\frac{b}{a} = \frac{b c}{a c}$ C、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ D、 $\frac{a b}{2 a b} = \frac{1}{2}$

查看试题解析
10. 把分式 $\frac{x - 3 y}{2 x} (x \neq 0 ， y \neq 0)$ 中的x、y缩小为原来的 $\frac{1}{2}$ ，那么分式的值（）

A、缩小2倍 B、扩大2倍 C、改变为原来的 $\frac{1}{4}$ D、不改变

查看试题解析

二、填空题

11. 函数 $y = \frac{3}{x + 2}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
12. 写出一个只含字母x的分式，且当x=9时，分式的值是－1，这个分式可以是．

查看试题解析
13. 把分式 $\frac{2}{3 a b^{2}} ， \frac{3}{2 a^{2}} ， \frac{1}{6 a b}$ 进行通分时，最简公分母为．

查看试题解析
14. 给出下列分式：
（1） $\frac{8 b c}{6 a}$ ，（2） $\frac{a^{2} + b^{2}}{a + b}$ ，（3） $\frac{4 a^{2} - b^{2}}{2 a - b}$ ，（4） $\frac{a - b}{b - a}$ ，（5） $\frac{a^{2} - b^{2}}{a^{2} + 2 a b + b^{2}}$ 其中最简分式有.（填序号）

查看试题解析
15. 如图，设k＝ $\frac{甲图中的阴影面积}{乙图中的阴影面积}$ (a＞b＞0)，则k＝.

查看试题解析

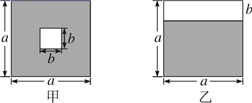
三、解答题

16. 已知 $\frac{1}{b} - \frac{1}{a}$ ＝5，求 $\frac{3 a + 2 a b - 3 b}{a - a b - b}$ 的值．

查看试题解析
17. 先化简，再求值：（ $\frac{a^{2}}{a - 1}$ ﹣a﹣1）÷ $\frac{a}{a^{2} - 1}$ ，其中a＝﹣2．

查看试题解析
18. 阅读下面材料，并解答问题.
将分式 $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式.

解：由分母为x²﹣1，可设x⁴+x²﹣3＝（x²﹣1）（x²+a）+b.

则x⁴+x²﹣3＝（x²﹣1）（x²+a）+b＝x⁴﹣x²+ax²﹣a+b＝x⁴+（a﹣1）x²﹣a+b

∴ ${\begin{cases} a - 1 = 1 \\ - a + b = - 3 \end{cases}$ ，∴ ${\begin{cases} a = 2 \\ b = - 1 \end{cases}$

∴ $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ ＝ $\frac{(x^{2} - 1) (x^{2} + 2) - 1}{x^{2} - 1}$ ＝ $\frac{(x^{2} - 1) (x^{2} + 2)}{x^{2} - 1}$ ﹣ $\frac{1}{x^{2} - 1}$ ＝（x²+2）﹣ $\frac{1}{x^{2} - 1}$

这样，分式 $\frac{x^{4} + x^{2} - 3}{x^{2} - 1}$ 被拆分成了一个整式x²+2与一个分式﹣ $\frac{1}{x^{2} - 1}$ 的和.

根据上述作法，将分式 $\frac{x^{4} + 6 x^{2} - 8}{x^{2} - 1}$ 拆分成一个整式与一个分式（分子为整数）的和的形式.

查看试题解析

四、综合题

19. 一般情况下，一个分式通过适当的变形，可以化为整式与分式的和的形式，例如：
① $\frac{x + 1}{x - 1}$ = $\frac{(x - 1) + 2}{x - 1}$ = $\frac{x - 1}{x - 1}$ + $\frac{2}{x - 1}$ =1+ $\frac{2}{x - 1}$ ；

② $\frac{x^{2}}{x - 2}$ = $\frac{x^{2} - 4 + 4}{x - 2}$ = $\frac{(x + 2) (x - 2) + 4}{x - 2}$ =x+2+ $\frac{4}{x - 2}$

(1)、试将分式 $\frac{x - 1}{x + 2}$ 化为一个整式与一个分式的和的形式；

(2)、如果分式 $\frac{2 x^{2} - 1}{x - 1}$ 的值为整数，求x的整数值．

查看试题解析
20. 小红、小刚、小明三位同学在讨论：当x取何整数时，分式 $\frac{3 x - 2}{x + 1}$ 的值是整数？
小红说：这个分式的分子、分母都含有x，它们的值均随x取值的变化而变化，有点难.
小刚说：我会解这类问题：当x取何整数时，分式 $\frac{3}{x + 1}$ 的值是整数？3是x+1的整数倍即可，注意不要忘记负数哦.
小明说：可将分式与分数进行类比.本题可以类比小学里学过的“假分数”，当分子大于分母时，可以将“假分数”化为一个整数与“真分数”的和.比如： $\frac{7}{3}$ ＝ $\frac{3 \times 2 + 1}{3}$ ＝2+ $\frac{1}{3}$ （通常写成带分数：2 $\frac{1}{3}$ ）.类比分式，当分子的次数大于或等于分母次数时，可称这样的分式为“假分式”，若将 $\frac{3 x - 2}{x + 1}$ 化成一个整式与一个“真分式”的和，就转化成小刚说的那类问题了！
小红、小刚说：对！我们试试看！…

(1)、解决小刚提出的问题；

(2)、解决他们共同讨论的问题.

查看试题解析
21.

(1)、因式分解：x²y﹣9y ．

(2)、化简 $\frac{x^{2} - 4 x}{x^{2} - 8 x + 16}$ ．

查看试题解析
22. 已知分式 $A = \frac{x}{x - 4} + \frac{y}{y - 4}$

(1)、已知 $x = 2 t + 6 ， y = 2 - 2 t (t \neq - 1)$ ，试求分式 $A$ 的值；

(2)、已知 $x = 3 y$ ，且分式 $A$ 的值等于2，试求 $x$ 以及 $y$ 的值；

(3)、已知 $x$ ， $y$ 均为正整数，试写出使分式 $A$ 的值等于2的所有 $x$ 以及 $y$ 的值.

查看试题解析
23. 综合题

(1)、不改变分式的值，使分式 $\frac{x - \frac{1}{3} y^{2}}{\frac{1}{2} x + y^{2}}$ 的分子与分母的各项的系数是整数.

(2)、不改变分式的值，使分式 $\frac{x - y^{2}}{x^{2} + y^{2}}$ 的分子与分母的最高次项的系数是正数.

(3)、当x满足什么条件时，分式 $\frac{2 - 3 x}{4 x^{2} + 1}$ 的值，①等于0?②小于0?

查看试题解析

（华师大版）2022-2023学年八年级数学下册16.1 分式及其基本性质 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（华师大版）2022-2023学年八年级数学下册16.1 分式及其基本性质同步测试