人教版九年级数学2023年寒假专项训练----复习部分第二十四章圆 B卷

试卷更新日期：2023-01-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 若⊙O 是以1为半径的圆，点M在圆内，则（）

A、 $O M < 1$ B、 $O M = 1$ C、 $O M > 1$ D、 $1 < O M < 2$

查看试题解析
2. 如图， $A B$ 为 $⊙ O$ 的直径，点C是弧 $B E$ 的中点．过点C作 $C D ⊥ A B$ 于点G，交 $⊙ O$ 于点D，若 $B E = 8 ， B G = 2$ ，则 $⊙ O$ 的半径长是（）

A、5 B、6.5 C、7.5 D、8

查看试题解析
3. 已知一个直角三角形的两条直角边的长恰好是方程 $x^{2} - 7 x ＋ 12 ＝ 0$ 的两个实数根，则该直角三角形外接圆的半径长为（）

A、3 B、4 C、6 D、2.5

查看试题解析
4. 在同圆中，下列命题正确的有（）
①平行弦所夹的弧相等；②三角形两个角的角平分线与外接圆的交点间的劣弧度数与第三个角的度数互补；③一个点到圆上各点的连线中，最大值为 $a$ ，最小值为 $b$ ，则圆的直径为 $a - b$ ；④若一个点到圆上不同三点的距离相等，则这个点一定是圆心．

A、4个 B、3个 C、2个 D、1个

查看试题解析
5. 如图，扇形 $O A B$ 中， $∠ A O B = 120 ° ， O A = 2$ ，点 $C$ 为 $O B$ 的中点，将扇形 $O A B$ 绕点 $C$ 顺时针旋转，点 $O$ 的对应点为 $O^{'}$ ，连接 $O^{'} B$ ，当 $O' C ∥ O A$ 时，阴影部分的面积为（）

A、 $\frac{π}{2} - \frac{\sqrt{3}}{2}$ B、 $\frac{2 π}{3} - \frac{2 \sqrt{3}}{3}$ C、 $\frac{π}{2} - \frac{\sqrt{3}}{3}$ D、 $\frac{2 π}{3} - \frac{\sqrt{3}}{2}$

查看试题解析
6. 如图，AB是半圆O的直径，点C、E是半圆上的动点（不与点A、B重合），且 $\overset{⌢}{A C}$ ＝ $\overset{⌢}{B E}$ ，射线AE，BC交于点F，M为AF中点，G为CM上一点，作∠GON＝ $\overset{⌢}{B C}$ ，交BC于点N，则点C在从点A往点B运动的过程中，四边形CGON的面积（）

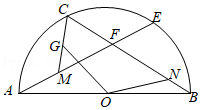A、先变大后变小 B、先变小后变大 C、保持不变 D、一直减小

查看试题解析
7. 如图，AB是⊙O的直径，点C，点D是半圆上两点，连结AC，BD相交于点P，连结AD，OD．已知OD⊥AC于点E，AB＝2．下列结论：
①AD²+AC²＝4；②∠DBC+∠ADO＝90°；③若AC＝BD，则DE＝OE；④若点P为BD的中点，则DE＝2OE．
其中正确的是（）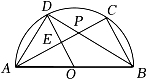

A、①②③ B、②③④ C、③④ D、②④

查看试题解析

二、填空题

8. 在正六边形ABCDEF中，对角线AC，BD相交于点M，则 $\frac{A M}{C M}$ 的值为.

查看试题解析
9. 如图， $A B 、 A C$ 分别为 $⊙ O$ 的内接正方形、内接正三角形的边， $B C$ 是圆内接正n边形的一边，则n的值为．

查看试题解析
10. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何？”意思是：今有一圆柱形木材，埋在墙壁中，不知其大小．用锯去锯这木材，锯口深 $E D = 1$ 寸，锯道长 $A B = 1$ 尺（1尺 $= 10$ 寸）．问这根圆形木材的直径是寸．

查看试题解析
11. 如图，弧AB所对圆心角∠AOB＝90°，半径为4，点C是OB中点，点D是弧AB上一点，CD绕点C逆时针旋转90°得到CE，则AE的最小值是.

查看试题解析
12. 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，OC，以下五个结论：①AD＝BE；②PQ∥AE；③AP＝BQ；④DE＝DP；⑤OC平分∠AOE．一定成立的结论有．

查看试题解析

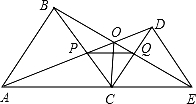
三、作图题

13. 【阅读理解】
六中珠江中学初三数学学习小组，在做《圆》的课题学习探究时发现：
三角形有五心：重心、外心、内心、垂心、旁心，其中的外心、内心、旁心是我们现在学习的《圆》的“心”．而找“心”所用的工具“垂直平分线”和“角平分线”是8年级学习内容．小组同学做了以下摘要记录
重心：三角形三条中线的交点叫做三角形重心，它是力的平衡点，重心是中线的三等分点．
外心：三角形外接圆的圆心，外心为三角形三边的垂直平分线的交点，外心到三顶点距离相等．
内心：三角形内切圆的圆心，内心为三角形三条内角平分线的交点，内心到三角形三边距离相等．
【实践探究】

(1)、已知 $△ A B C$ 中， $A B = 20$ ， $A C = 13$ ， $B C = 21$
①作出 $△ A B C$ 的角平分线交点 $O$ （尺规作图，不写作法，保留作图痕迹）；
过 $O$ 作 $O M ⊥ B C$ ，垂足为 $M$ （不需尺规作图）；
以 $O$ 为圆心， $O M$ 为半径作出 $△ A B C$ 的内切圆
②求出 $△ A B C$ 的面积．
③求出内切圆 $⊙ O$ 的半径 $R$ 的长度．

(2)、已知 $△ A B C$ 中， $A B = 2 \sqrt{5}$ ， $A C = 4 \sqrt{2}$ ， $B C = 6$ ，
①作出 $△ A B C$ 的三边垂直平分线的交点 $O$ （尺规作图，不写作法，保留作图痕迹）；
连接 $A O$ ；以 $O$ 为圆心， $A O$ 为半径作出 $△ A B C$ 的外接圆
②以 $B$ 为原点， $B C$ 所在的直线为 $x$ 轴（点 $C$ 在点 $B$ 右方）建立直角坐标系，求点A坐标．
③求出外接圆 $⊙ O$ 的半径 $R$ 的长度．

查看试题解析

四、综合题

14. 已知钝角三角形 $A B C$ 内接于 $⊙ O ， E 、 D$ 分别为 $A C 、 B C$ 的中点，连接 $D E$ .

(1)、如图1，当点 $A 、 D 、 O$ 在同一条直线上时，求证： $D E = \frac{1}{2} A C$ .

(2)、如图2，当 $A 、 D 、 O$ 不在同一条直线上时，取 $A O$ 的中点 $F$ ，连接 $F D$ 交 $A C$ 于点 $G$ ，当 $A B + A C = 2 A G$ 时.
①求证： $△ D E G$ 是等腰三角形；
②如图3，连 $O D$ 并延长交 $⊙ O$ 于点 $H$ ，连接 $A H$ .求证： $A H ∥ F G$ .

查看试题解析
15. 数学活动课上，老师给出这样一个题目：如图1，点C是弧 $A B$ 上的点， $C D ⊥ O A$ 于D， $C E ⊥ O B$ 于E，若 $C D = C E$ ，求证：点C是弧 $A B$ 的中点.
小波同学想到的办法是：可通过证明 $△ C D O ≌ △ C E O$ 来完成它.

(1)、请你们帮助小波完成证明过程：

(2)、解答完老师给出的问题后，小波把老师的题进行了改变.
如图2，已知 $C H$ 是 $⊙ O$ 的直径，点D，点E分别是半径 $O A$ ， $O B$ 的中点，延长 $C E$ 交 $B H$ 于点F，若 $C D ⊥ O A$ 于D，且点C是弧 $A B$ 的中点，求证： $F C = F H$ ，请你证明.

(3)、拓展：如图3，在（2）的条件下，点G是弧 $B H$ 上一点，连接 $A G ， B G ， H G$ ， $O F$ ，若 $H G = 4$ ， $A G ： B G = 5 ： 3$ ，求 $⊙ O$ 的半径长.

查看试题解析
16. 如图，点P是等边三角形 $A B C$ 中 $A C$ 边上的动点（ $0 ° < ∠ A B P < 30 °$ ），作 $△ B C P$ 的外接圆交 $A B$ 于点D.点E是圆上一点，且 $\overset{⌢}{P D} = \overset{⌢}{P E}$ ，连接 $D E$ 交 $B P$ 于点F.

(1)、求证： $B E = B C$

(2)、当点P运动变化时， $∠ B F D$ 的度数是否发生变化？若变化，请说明理由；若不变，求 $∠ B F D$ 的度数.

(3)、探究线段 $B F$ 、 $C E$ 、 $E F$ 之间的数量关系，并证明.

查看试题解析
17. 请阅读下列材料，并完成相应的任务：阿基米德折弦定理，阿基米德（公元前287年一公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯，牛顿并列为世界三大数学家．
阿拉伯Al-Binmi（973年一1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．

阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是 $\overset{⌢}{A B C}$ 的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD＝AB+BD．

小明同学运用“截长法”和三角形全等来证明CD＝AB+BD，过程如下：

证明：如图2所示，在CB上截取CG＝AB，连接MA，MB，MC和MG．

∵M是 $\overset{⌢}{A B C}$ 的中点，∴MA＝MC，…

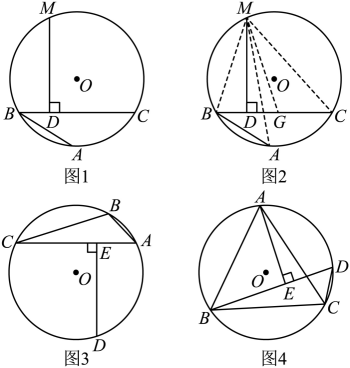(1)、请按照上述思路，写出该证明的剩余部分；

(2)、如图3，在⊙O中，BD =CD，DE⊥AC，若AB = 4，AC = 10，则AE的长度为；

(3)、如图4，已知等边 $△$ ABC内接于⊙O，AB = 8，D为 $\overset{⌢}{A C}$ 上一点，∠ABD = 45°，AE⊥BD于点E，求 $△$ BDC的周长．

查看试题解析

人教版九年级数学2023年寒假专项训练----复习部分 第二十四章 圆 B卷

一、单选题

二、填空题

三、作图题

四、综合题

人教版九年级数学2023年寒假专项训练----复习部分第二十四章圆 B卷