人教版九年级数学2023年寒假专项训练----复习部分第二十三章旋转 B卷

试卷更新日期：2023-01-12 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（）．

A、60° B、90° C、120° D、150°

查看试题解析
2. 如图，在平面直角坐标系中，画 $△ A B C$ 关于点O成中心对称的图形时，由于紧张对称中心选错，画出的图形是 $△ D E F$ ，请你找出此时的对称中心是（）

A、 $(2 ， 0)$ B、 $(2 ， 1)$ C、 $(1 ， 2)$ D、 $(1 ， 0)$

查看试题解析
3. 如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（）

A、34° B、36° C、38° D、40°

查看试题解析
4. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE，若点D在线段BC的延长线上，则∠B的大小为（）

A、 $6 0^{∘}$ B、 $5 0^{∘}$ C、 $4 5^{∘}$ D、 $4 0^{∘}$

查看试题解析
5. 如图，点E是正方形 $A B C D$ 的边 $D C$ 上一点，把 $△ A D E$ 绕点A顺时针旋转 $90 °$ 到 $△ A B F$ 位置．若四边形 $A E C F$ 的面积为36， $D E = 2$ ，则 $A E$ 的长为（）

A、 $4 \sqrt{2}$ B、 $2 \sqrt{6}$ C、6 D、 $2 \sqrt{10}$

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A C B = 30 °$ ，将 $△ A B C$ 绕点 $C$ 顺时针旋转 $60 °$ 得到 $△ D E C$ ，点A、B的对应点分别是 $D$ ， $E$ ，点 $F$ 是边 $A C$ 的中点，连接 $B F$ ， $B E$ ， $F D$ .则下列结论错误的是（）

A、 $B E = B C$ B、 $B F ∥ D E$ ， $B F = D E$ C、 $∠ D F C = 90 °$ D、 $D G = 3 G F$

查看试题解析
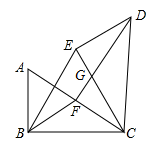7. 如图，正方形ABCD对角线的交点刚好在坐标原点，其中点D坐标为（1，1），若将对角线BD绕点B逆时针旋转30°后所在的直线交y轴于点E，连接AE．下列4个结论：
①点O到直线BE的距离为 $\frac{\sqrt{2}}{2}$ ；②OE的长为 $\sqrt{2} + 1$ ；③AB=AE；④直线AE的解析

式为y= $\sqrt{3}$ x+ $\sqrt{3}$ +1．其中正确的是（）

A、①④ B、②④ C、①②③ D、①③④

查看试题解析

二、填空题

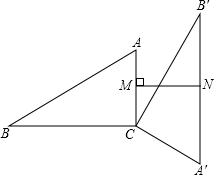
8. 如果点 $M (x ， y)$ 关于原点的对称点为 $(- 2023 ， - 1)$ ，则 $x + y =$ ．

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C顺时针旋转得到△A'B'C，M是AC的中点，N是A'B'的中点，连接MN，若AC＝4，∠ABC＝30°，则线段MN的最小值为．

查看试题解析
10. 如图，菱形ABCD和菱形AEFG开始完全重合，现将菱形AEFG绕点A顺时针旋转，设旋转角∠BAE=α（0°＜α＜360°），则当α=时，菱形的顶点F会落在菱形ABCD的对角线所在的直线上．

查看试题解析
11. 如图，在Rt $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 6$ ， $A C = \sqrt{15}$ ， $C D$ 是斜边 $A B$ 的中线，将 $△ A B C$ 绕点A旋转，点B、C的对应点分别是点E、F，如果点F在射线 $C D$ 上，那么 $\frac{S_{Δ A D F}}{S_{Δ A E F}}$ ＝．

查看试题解析

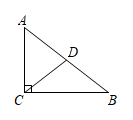
三、作图题

12. 如图，在下列 $8 \times 8$ 的网格中，横、纵坐标均为整点的数叫做格点， $△ A B C$ 的顶点的坐标分别为 $A (3 ， 0)$ ， $B (0 ， 4)$ ， $C (4 ， 2)$ .

⑴直接写出 $△ A B C$ 的形状；

⑵要求在下图中仅用无刻度的直尺作图：将 $△ A B C$ 绕点 $B$ 逆时针旋转角度 $2 α$ 得到 $△ A_{1} B C_{1}$ ，其中 $α = ∠ A B C$ ， $A$ ， $C$ 的对应点分别为 $A_{1}$ ， $C_{1}$ ，请你完成作图；

⑶在网格中找一个格点 $G$ ，使得 $C_{1} G ⊥ A B$ ，并直接写出 $G$ 点的坐标；

⑷作点 $C_{1}$ 关于 $B C$ 的对称点 $D$ .

查看试题解析

四、解答题

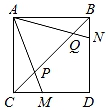
13. 如图，已知正方形ABCD，∠MAN＝45°，连接CB，交AM、AN分别于点P、Q，求证：CP²+BQ²＝PQ².

查看试题解析
14. 在△ABC中AB=AC，点P在平面内，连接AP并将线段AP绕点A顺时针方向旋转与∠BAC相等的角度，得到线段AQ，连接BQ；

【发现问题】如图1，如果点P是BC边上任意一点，则线段BQ和线段PC的数量关系是 ▲ ；

【探究猜想】如图2，如果点P为平面内任意一点，前面发现的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由.请仅以图2所示的位置关系加以证明（或说明）；

【拓展应用】如图3，在△ABC中，AC=2，∠ACB=90°，∠ABC=30°，P是线段BC上的任意一点连接AP，将线段AP绕点A顺时针方向旋转60°，得到线段AQ，连接CQ，请直接写出线段CQ长度的最小值.

查看试题解析

五、综合题

15. 如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG．

(1)、如图1，若AD＝2 $\sqrt{3}$ 、DE＝2，当 $∠ A D G ＝ 150 °$ 时，求AG的长；

(2)、如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE之间有何等量关系？并利用图2加以证明．

查看试题解析
16. 综合与实践
某学校的数学兴趣小组发现这样一个模型，两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来，会形成一组全等的三角形，具有这个规律的图形称为“手拉手”图形．

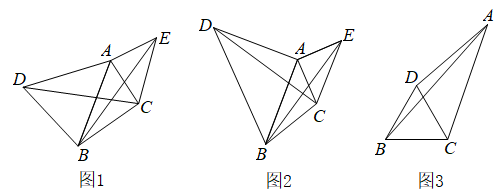(1)、[材料理解]如图1，在 $△ A B C$ 中，分别以 $A B$ ， $A C$ 为边向外作等腰 $△ A B D$ 和等腰 $△ A C E$ ． $A B ＝ A D$ ， $A C ＝ A E$ ， $∠ B A D = ∠ C A E$ ，连接 $B E$ ， $C D$ ，试猜想 $B E$ 与 $C D$ 的大小关系，并说明理由；

(2)、[深入探究]如图2，在 $△ A B C$ 中， $A B ＝ 6$ ， $B C ＝ 4$ ， $∠ A B C ＝ 45 °$ ，分别以 $A B$ ， $A C$ 为边向外作等腰直角 $△ A B D$ 和等腰直角 $△ A B C$ ， $∠ B A D ＝ ∠ C A E ＝ 90 °$ ，连接 $B E$ ， $C D$ ，求 $B E$ 的长．

(3)、[延伸应用]如图3，在 $△ A B C$ 中， $A B ＝ 10$ ，点D为平面内一点，连接 $A D$ ， $B D$ ，满足 $A D ＝ 6$ ， $B D ＝ B C$ ， $∠ D B C ＝ 60 °$ ， $∠ D A C ＝ 30 °$ ，求 $A C$ 的长．

查看试题解析
17. 已知△ABC为等边三角形，其边长为4．点P是AB边上一动点，连接CP．

(1)、如图1，点E在AC边上且AE＝BP，连接BE交CP于点F．
①求证：BE＝CP；
②求∠BFC的度数．

(2)、如图2，将线段CP绕点C顺时针旋转120°得线段CQ，连接BQ交AC于点D．设BP＝x，CD＝y，求y与x的函数关系式．

查看试题解析

人教版九年级数学2023年寒假专项训练----复习部分 第二十三章 旋转 B卷

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

人教版九年级数学2023年寒假专项训练----复习部分第二十三章旋转 B卷