人教版九年级数学2023年寒假专项训练----复习部分 第二十四章 圆 A卷
试卷更新日期:2023-01-12 类型:复习试卷
一、单选题
-
1. 如图, 一块直角三角板的角的顶点落在上, 两边分别交于两点, 连结 , 则的度数是( )
 A、 B、 C、 D、2. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
A、 B、 C、 D、2. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( ) A、 B、 C、2π D、3. 我国古代数学名作《九章算术》中记载了“圆材埋壁”问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其大意为:如图,现有圆柱状的木材埋在墙壁里,不知道其宽度的大小,于是用锯子(沿横截面)锯它,当量得深度CE=1寸的时候,锯开的宽度AB=1尺(1尺=10寸),问木材的直径CD的长是( )
A、 B、 C、2π D、3. 我国古代数学名作《九章算术》中记载了“圆材埋壁”问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”其大意为:如图,现有圆柱状的木材埋在墙壁里,不知道其宽度的大小,于是用锯子(沿横截面)锯它,当量得深度CE=1寸的时候,锯开的宽度AB=1尺(1尺=10寸),问木材的直径CD的长是( ) A、寸 B、10寸 C、13寸 D、26寸4. 已知⊙O的半径是3,点P在圆外,则线段OP的长可能是( )A、1 B、2 C、3 D、45. 下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有( )A、①④ B、②③ C、①③ D、②④6. 如图,AB是半圆O的直径,点D是弧AC的中点,若∠BAC=44°,则∠DAC等于( )
A、寸 B、10寸 C、13寸 D、26寸4. 已知⊙O的半径是3,点P在圆外,则线段OP的长可能是( )A、1 B、2 C、3 D、45. 下列有关圆的一些结论:①平分弧的直径垂直于弧所对的弦;②平分弦的直径垂直于弦;③在同圆或等圆中,相等的弦所对的圆周角相等;④同弧或等弧所对的弦相等,其中正确的有( )A、①④ B、②③ C、①③ D、②④6. 如图,AB是半圆O的直径,点D是弧AC的中点,若∠BAC=44°,则∠DAC等于( )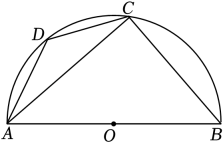 A、22° B、44° C、23° D、46°7. 如图,阴影部分是某个品牌商标的图案,为了研究它的面积,小明通过数学知识找到弧所在圆的圆心 , 经测量 , , 则商标的面积为( )
A、22° B、44° C、23° D、46°7. 如图,阴影部分是某个品牌商标的图案,为了研究它的面积,小明通过数学知识找到弧所在圆的圆心 , 经测量 , , 则商标的面积为( ) A、 B、 C、 D、8. 如图,圆上有两点 , , 连结 , 分别以 , 为圆心,的长为半径画弧,两弧相交于点交于点E,交于点F,若 , 则该圆的半径长是( )
A、 B、 C、 D、8. 如图,圆上有两点 , , 连结 , 分别以 , 为圆心,的长为半径画弧,两弧相交于点交于点E,交于点F,若 , 则该圆的半径长是( ) A、10 B、6 C、5 D、4
A、10 B、6 C、5 D、4二、填空题
-
9. 在同一平面内,点P到的最长距离为 , 最短距离为 , 则的半径为.10. 如图,中, , 则.
 11. 如图,内接于半径为的半 , 为直径,点是的中点,连接交于点 , 平分交于点 , 且为的中点,则的长为.
11. 如图,内接于半径为的半 , 为直径,点是的中点,连接交于点 , 平分交于点 , 且为的中点,则的长为.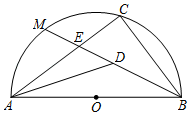 12. 如图,是的直径, , 是的半径, , 点在上, , 点是半径上的一个动点,则的最小值为.
12. 如图,是的直径, , 是的半径, , 点在上, , 点是半径上的一个动点,则的最小值为. 13. 如图,在矩形ABCD中,AB=3,对角线AC,BD的交点为O,分别以A、D为圆心,AB的长为半径画弧,恰好经过点O,则图中阴影部分的面积为.(结果保留π)
13. 如图,在矩形ABCD中,AB=3,对角线AC,BD的交点为O,分别以A、D为圆心,AB的长为半径画弧,恰好经过点O,则图中阴影部分的面积为.(结果保留π)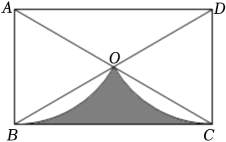
三、解答题
-
14. 如图,圆是的内切圆,其中 , , 求其内切圆的半径.
 15. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.
15. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.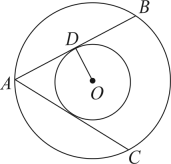 16. 根据以下素材,探索完成任务.
16. 根据以下素材,探索完成任务.如何确定隧道的限高?
素材1
从小清家到附近山区的一条双行线公路上有一个隧道,在隧道口有一个限高标志(如图1),表示禁止装载高度(车顶最高处到地面)超过的车辆通行.那么这个限高是如何确定的呢?

素材2
小清通过实地调查和查阅相关资料,获得以下信息:
①隧道的横截面成轴对称,由一个矩形和一个弓形构成.
②隧道内的总宽度为 , 双行车道宽度为 , 隧道圆拱内壁最高处距路面 , 矩形的高为 , 车道两侧的人行道宽.
③为了保证安全,交通部门要求行驶车辆的顶部(设为平顶)与隧道圆拱内壁在竖直方向上的高度差相差最少.

问题解决
任务1
计算半径
求图1中弓形所在圆的半径.
任务2
确定限高
如图2,在安全的条件下,的限高是如何确定的?请通过计算说明理由.(参考数据: , 结果保留一位小数)
任务3
尝试设计
如果要使高度不超过 , 宽为的货车能顺利通过这个隧道,且不改变隧道内的总宽度()和矩形的高(),如何设计隧道的弓形部分(求弓形所在圆的半径至少为多少米?)(参考数据: , 结果保留一位小数)