人教版九年级数学2023年寒假专项训练----复习部分 第二十二章 二次函数 B卷
试卷更新日期:2023-01-12 类型:复习试卷
一、单选题
-
1. 二次函数的图象经过点 , 则代数式的值为 ( )A、-1 B、0 C、1 D、22. 已知二次函数的x、y的部分对应值如下表:
x
-1
0
1
2
3
y
5
1
-1
-1
1
下列结论中正确的有( )个.
①;②抛物线的对称轴是直线;③不等式的解集是;④1是方程的根.
A、1个 B、2个 C、3个 D、4个3. 已知二次函数 , 若 , 且 , 则它的图象可能是( )A、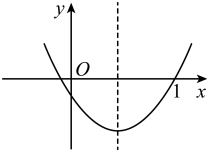 B、
B、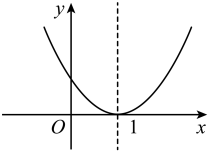 C、
C、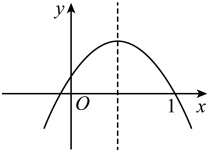 D、
D、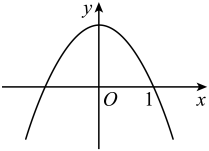 4. 将抛物线向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )A、 B、y=(x-4)2+4 C、 D、5. 如图,二次函数与一次函数的图像可能是( )A、
4. 将抛物线向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为( )A、 B、y=(x-4)2+4 C、 D、5. 如图,二次函数与一次函数的图像可能是( )A、 B、
B、 C、
C、 D、
D、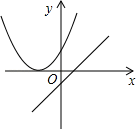 6. 如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(-4,1),(-1,-4),且AD平行于x轴,当函数y=x2+2mx-2(x≤0)的图象在矩形ABCD内部的部分均为y随x的增大而减小时,下列选项中符合条件的m的取值范围为( )
6. 如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(-4,1),(-1,-4),且AD平行于x轴,当函数y=x2+2mx-2(x≤0)的图象在矩形ABCD内部的部分均为y随x的增大而减小时,下列选项中符合条件的m的取值范围为( )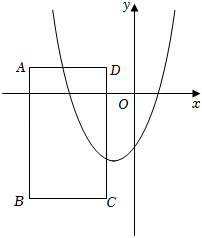 A、1≤m≤ B、0≤m≤ C、-1<m≤1或≤m< D、-1<m≤0或1≤m<7. 二次函数y=ax2十bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①;②;③c-4a=1;④;⑤(m为任意实数).其中正确的有( )
A、1≤m≤ B、0≤m≤ C、-1<m≤1或≤m< D、-1<m≤0或1≤m<7. 二次函数y=ax2十bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①;②;③c-4a=1;④;⑤(m为任意实数).其中正确的有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
8. 如图,与轴交于 , 两点(在左边)与轴交于点,是线段上的一点,连结交轴于点 , 连结 , 当和的面积之和与的面积相等时,点的坐标为.
 9. 大强对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为 , 由此可知大强此次实心球训练的成绩为米.
9. 大强对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为 , 由此可知大强此次实心球训练的成绩为米. 10. 已知二次函数y=a(x-x1)(x-x2)与x轴的交点是(1,0)和(3,0),关于x的方程a(x-x1)(x-x2)=m(m>0)的两个解分别为-1和5,关于x的方程a(x-x1)(x-x2)=n(其中m>n>0)也有两个整数解,则这两个整数解分别是 .11. 已知关于x的方程 的两个根分别是 , , 若点P是二次函数 的图象与y轴的交点,过P作轴交抛物线于另一交点Q,则PQ的长为 .
10. 已知二次函数y=a(x-x1)(x-x2)与x轴的交点是(1,0)和(3,0),关于x的方程a(x-x1)(x-x2)=m(m>0)的两个解分别为-1和5,关于x的方程a(x-x1)(x-x2)=n(其中m>n>0)也有两个整数解,则这两个整数解分别是 .11. 已知关于x的方程 的两个根分别是 , , 若点P是二次函数 的图象与y轴的交点,过P作轴交抛物线于另一交点Q,则PQ的长为 .三、解答题
-
12. 如图所示,在抛物线上选定两点,我们把过这两点的线段和这条抛物线所围成的图形称作抛物线弓形.在平面直角坐标系 中,已知抛物线 与直线 相交于点O和点A , 截得的抛物线弓形的曲线上有一点P .

(Ⅰ)当 时,解答下列问题:
①求A点的坐标;
②连接 , ,求 面积的最大值;
③当 的面积最大时,直线 也截得一个更小的抛物线弓形,同理在这个更小的抛物线弓形曲线上也有一点 ,连接 , ,当 的面积最大时,求这个 的最大面积与②中 的最大面积的比值;
(Ⅱ)将(Ⅰ)中 的条件去掉后,其它条件不变,则 的最大面积与 的最大面积的比值是否变化?请说明理由.
13. 根据以下素材,探索完成任务.如何设计喷泉喷头的升降方案?
素材1
如图1,湖中有一个可垂直升降的喷泉,喷出的水柱呈抛物线.记水柱上某一点到喷头的水平距离为x米,到湖面的垂直高度为y米.当喷头位于起始位置时,测量得x与y的四组数据如下:
x(米)
0
2
3
4
y(米)
1
2
1.75
1

素材2
公园想设立新的游玩项目,通过升降喷头,使游船能从水柱下方通过,如图2,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚宽度为3米,顶棚到湖面的高度为2米.
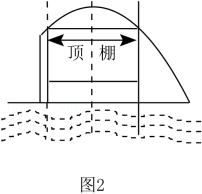
问题解决
任务1
确定喷泉形状
结合素材1,求y关于x的表达式.
任务2
探究喷头升降方案
为使游船按素材2要求顺利通过,求喷头距离湖面高度的最小值.
14. 在校运动会上,小华在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是米,当铅球运行的水平距离为4米时,达到最大高度3米的B处.小华此次投掷的成绩是多少米?
四、综合题
-
15. 已知函数 , 在同一平面直角坐标系中.(1)、若经过点(1,-2),求的函数表达式.(2)、若经过点(1,m+1),判断与图象交点的个数,说明理由.(3)、若y1经过点( , 0),且对任意x,都有 , 请利用图象求a的取值范围.16. 已知,如图抛物线与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为 , .
 (1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形AOCD面积的最大值;(3)、若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.17. 平面直角坐标系中,抛物线与直线交于点 , , 与y轴交于点C.
(1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形AOCD面积的最大值;(3)、若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.17. 平面直角坐标系中,抛物线与直线交于点 , , 与y轴交于点C.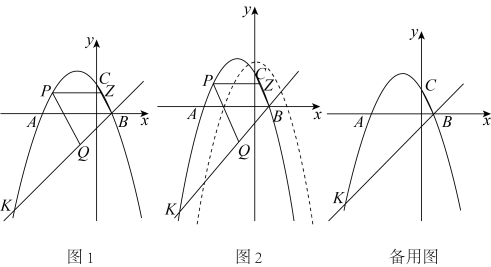 (1)、求抛物线的函数表达式及顶点坐标;(2)、如图1,连接 , 点P是线段上方抛物线上的一个动点,过点P作PZx轴交于点Z,过点P作PQCB交直线于点Q,求的最大值及此时点P的坐标;(3)、如图2,在(2)的条件下,将该抛物线向下平移个单位,向右平移3个单位,使得P点对应点.点S是新抛物线对称轴上一点,在平面上否存在一点N,使以、S、A、N为顶点的四边形是菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的函数表达式及顶点坐标;(2)、如图1,连接 , 点P是线段上方抛物线上的一个动点,过点P作PZx轴交于点Z,过点P作PQCB交直线于点Q,求的最大值及此时点P的坐标;(3)、如图2,在(2)的条件下,将该抛物线向下平移个单位,向右平移3个单位,使得P点对应点.点S是新抛物线对称轴上一点,在平面上否存在一点N,使以、S、A、N为顶点的四边形是菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.