初中数学同步训练必刷题（人教版七年级下册 5.1.3 同位角、内错角、同旁内角）
试卷更新日期：2023-01-12 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 如图所示，在所标识的角中，内错角是（ ）
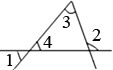A、和 B、和 C、和 D、和2. 如图，直线a，b被c所截，则与是（ ）
A、同位角 B、内错角 C、同旁内角 D、邻补角3. 如图，图中的∠1与∠2是（ ）．
A、对顶角 B、同位角 C、内错角 D、同旁内角4. 如图，已知两条直线被第三条直线所截，则下列说法正确的是（ ）
A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角5. 下列说法错误的是（ ）A、对顶角相等 B、同位角相等 C、同角的余角相等 D、同角的补角相等6. 如图，下列说法错误的是（ ）
A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角7. 下列图形中， 与 是同位角的有（ ）
A、①② B、①③ C、②③ D、②④8. 中国滑雪天才少女谷爱凌在2022年北京冬奥会的赛场上斩获“自由式滑雪大跳台”首金，这是她获得的首个冬奥会奖牌，也是中国运动员第一次参加冬奥会大跳台的比赛．项目图标如下图；则在下列判断中①∠1与∠2是对顶角；②∠3与∠4是同旁内角；③∠5与∠6是同旁内角；④∠1与∠4是内错角，其中正确的有（ ）个．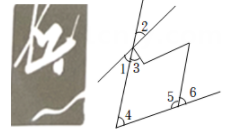
A、1 B、2 C、3 D、49. 如图，说法正确的是（ ）
A、和是内错角 B、和是内错角 C、和是同位角 D、和是同旁内角10. 如图，按各组角的位置判断错误的是（ ）
A、∠1与∠4是同旁内角 B、∠3与∠4是内错角 C、∠5与∠6是同旁内角 D、∠2与∠5是同位角二、填空题（每题3分，共30分）
-
11. 如图，直线、被直线所截，交点分别为M、N，则的同位角是.
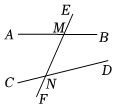12. 如图，直线a、b被直线c所截，则与是内错角．
13. 如图，直线a，b被直线c所截， 的同旁内角是 ．
14. 如图，与是直线和直线被直线所截形成的 ．
15. 如图，下列结论：①∠2与∠3是内错角；②∠1与∠A是同位角；③∠A与∠B是同旁内角；④∠B与∠ACB不是同旁内角，其中正确的是 .（只填序号）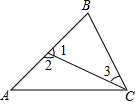
16. 如图，“4”字图中有a对同位角，b对内错角，c对同旁内角，则abc= ．
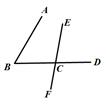17. 如图，下列结论：① 与 是内错角；② 与 是同位角；③ 与 是同旁内角；④ 与 不是同旁内角，其中正确的是（只填序号）.
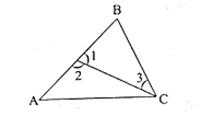18. 如图，与∠A 是同旁内角的角共有个．
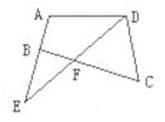19. 在我们生活的现实世界中，随处可见由线交织而成的图．下图是七年级教材封面上的相交直线，则∠1的同位角是 ．
20. 如图，有下列3个结论：①能与∠DEF构成内错角的角的个数是2；②能与∠EFB构成同位角的角的个数是1；③能与∠C构成同旁内角的角的个数是4，以上结论正确的是.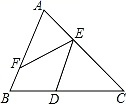
三、解答题（共8题，共60分）
-
21. 如图，指出图中直线AC ， BC被直线AB所截的同位角、内错角、同旁内角．
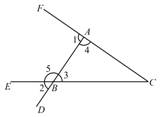22. 如图所示，∠1与∠2，∠3与∠4之间各是哪两条直线被哪一条直线所截而形成的什么角？
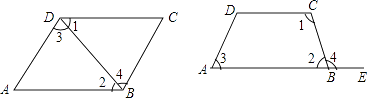23. 如图，直线AD与AE相交于点A，直线BC分别交AD、AE于点B、C，直线DE分别交AD、AE于点D、E，分别写出图中的两对同位角、两对内错角、两对同旁内角．
24.如图，∠1，∠2，∠3，∠4及∠A，∠B，∠C中有多少对同位角、内错角、同旁内角？请一一写出来．
25. 如图所示，回答下列问题．
(1)、请写出直线AB．CD被AC所截形成的内错角；(2)、请写出直线AB．CD被BE所截形成的同位角；(3)、找出图中∠1的所有同旁内角．26. 如图，在已标出的五个角中，
(1)、直线AC，BD被直线ED所截，∠1与是同位角；(2)、∠1与∠4是直线 ， 被直线所截得的内错角；(3)、∠2与是直线AB，被直线所截得的同旁内角．27. 已知：如图是一个跳棋棋盘，其游戏规则是一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置跳到终点位置有两种不同路径，路径1：；路径2：.
试一试：
(1)、写出从起始位置跳到终点位置的一种路径；(2)、从起始位置依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置？28. 复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．
(1)、如图1，直线 ， 被直线 所截，在这个基本图形中，形成了对同旁内角．(2)、如图2，平面内三条直线 ， ， 两两相交，交点分别为A、B、C，图中一共有对同旁内角．(3)、平面内四条直线两两相交，最多可以形成对同旁内角．(4)、平面内n条直线两两相交，最多可以形成对同旁内角．