初中数学同步训练必刷题(人教版七年级下册5.1.1 相交线)
试卷更新日期:2023-01-12 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列四个图形中,与是对顶角的是()A、
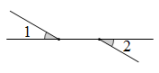 B、
B、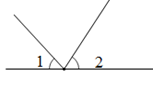 C、
C、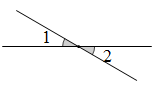 D、
D、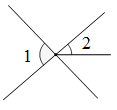 2. 直线AB和直线CD相交于点O,若∠AOC=40°,则∠BOC等于( )
2. 直线AB和直线CD相交于点O,若∠AOC=40°,则∠BOC等于( ) A、140° B、60° C、40° D、160°3. 如图,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,则∠BOD等于( )
A、140° B、60° C、40° D、160°3. 如图,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,则∠BOD等于( ) A、36° B、72° C、60° D、75°(4. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( )
A、36° B、72° C、60° D、75°(4. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( ) A、115° B、125° C、135° D、145°5. 如图,小明手持手电筒照向地面,手电筒发出的光线CO与地面AB形成了两个角,∠BOC=8∠AOC , 则∠BOC的度数是( )
A、115° B、125° C、135° D、145°5. 如图,小明手持手电筒照向地面,手电筒发出的光线CO与地面AB形成了两个角,∠BOC=8∠AOC , 则∠BOC的度数是( )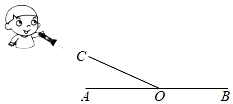 A、160° B、150° C、120° D、20°6. 如图,直线AB , CD相交于点O , 如果∠1=35°,那么∠2的度数是( )
A、160° B、150° C、120° D、20°6. 如图,直线AB , CD相交于点O , 如果∠1=35°,那么∠2的度数是( ) A、 B、 C、 D、7. 如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD的度数为( )
A、 B、 C、 D、7. 如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD=2:3,则∠BOD的度数为( ) A、40° B、37° C、36° D、35°8. 如图,直线、相交于点 , 且 , 则的度数为( )
A、40° B、37° C、36° D、35°8. 如图,直线、相交于点 , 且 , 则的度数为( ) A、 B、 C、 D、9. 如图,直线AB、CD相交于点O,下列描述一定正确的是( )
A、 B、 C、 D、9. 如图,直线AB、CD相交于点O,下列描述一定正确的是( ) A、∠1和∠2互为对顶角 B、∠1和∠3互为邻补角 C、∠1=∠2 D、∠1=∠310. 如图,直线AB、CD相交于O,OA平分∠EOC,若 , 那么∠BOD的度数是( )
A、∠1和∠2互为对顶角 B、∠1和∠3互为邻补角 C、∠1=∠2 D、∠1=∠310. 如图,直线AB、CD相交于O,OA平分∠EOC,若 , 那么∠BOD的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共30分)
-
11. 若∠1和∠2是对顶角,∠1=36°,则∠2的度数是度.12. 如图,与是对顶角, , , 则°.
 13. 如图,直线AB,CD相交于点O,OE是∠AOD的平分线,若∠BOD=40°,则∠COE的度数为 .
13. 如图,直线AB,CD相交于点O,OE是∠AOD的平分线,若∠BOD=40°,则∠COE的度数为 . 14. 若与是对顶角,与互余,且 , 则的度数为°.15. 如图,直线AB、CD相交于点O,OE平分 , OF平分 . 若 , 则的度数为°.
14. 若与是对顶角,与互余,且 , 则的度数为°.15. 如图,直线AB、CD相交于点O,OE平分 , OF平分 . 若 , 则的度数为°. 16. 如图,点 O 在直线 AB 上,过点 O 作射线 OC,若∠AOC=53°17′28″,则∠BOC 的度数是 .
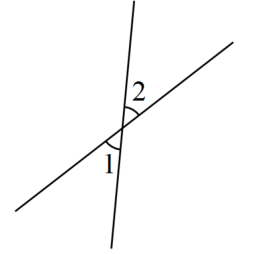
16. 如图,点 O 在直线 AB 上,过点 O 作射线 OC,若∠AOC=53°17′28″,则∠BOC 的度数是 . 17. 在同一平面内的三条直线,它们的交点个数可能是 .18. 如图,两直线交于点O,若∠3=3∠2,则∠1的度数是 .
17. 在同一平面内的三条直线,它们的交点个数可能是 .18. 如图,两直线交于点O,若∠3=3∠2,则∠1的度数是 . 19. 如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得 的度数就是 的度数.其中的数学原理是 .
19. 如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得 的度数就是 的度数.其中的数学原理是 .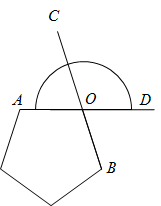 20. 小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板 ,并将边 延长至点 ,第二步将另一块三角板 的直角顶点与三角板 的直角顶点 重合,摆放成如图所示,延长 至点 , 与 就是一组对顶角,若 ,则 , 若重叠所成的 ,则 的度数 .
20. 小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板 ,并将边 延长至点 ,第二步将另一块三角板 的直角顶点与三角板 的直角顶点 重合,摆放成如图所示,延长 至点 , 与 就是一组对顶角,若 ,则 , 若重叠所成的 ,则 的度数 .
三、解答题(共8题,共60分)
-
21. 如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=72°,求∠AOF的度数.
 22. 如图,直线 , 相交于点 , , ,求 的度数.
22. 如图,直线 , 相交于点 , , ,求 的度数. 23. 如图,直线a,b相交于点O,已知 , 求的度数.
23. 如图,直线a,b相交于点O,已知 , 求的度数. 24. 如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.
24. 如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.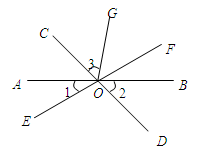 25. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.
25. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°. (1)、求∠DOE的度数;(2)、求∠EOF的度数.
(1)、求∠DOE的度数;(2)、求∠EOF的度数.


