鲁教版（五四学制）2022-2023学年八年级数学下册7.2 二次根式的性质同步测试

试卷更新日期：2023-01-11 类型：同步测试

进入出卷网下载

一、单选题

1. 实数 $a 、 b$ 在数轴上的位置如图所示，请化简： $\sqrt{a^{2}} - \sqrt{b^{2}}$ =（）

A、 $a - b$ B、 $- a + b$ C、 $- a - b$ D、 $a + b$

查看试题解析
2. 下列四个等式：① $\sqrt{(- 4)^{2}} = 4$ ；②（- $\sqrt{4}$ ）²＝16；③（ $\sqrt{4}$ ）²＝4；④ $\sqrt{(- 4)^{2}} = - 4$ ．正确的是（　　）

A、①② B、③④ C、②④ D、①③

查看试题解析
3. 下列各式中，化简正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 ${(\sqrt{3})}^{2} = 9$ C、 ${(\sqrt[3]{- 3})}^{3} = 27$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
4. 在 $\sqrt{1.5}$ ， $\sqrt{30}$ ， $\sqrt{\frac{1}{2}}$ ， $\sqrt{12}$ 中最简二次根式的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 已知n是一个正整数，且 $\sqrt{24 n}$ 是整数，那么n的最小值是（）

A、6 B、36 C、3 D、2

查看试题解析
6. 下列二次根式中与 $\sqrt{a + 1}$ 互为有理化因式的是（）

A、 $\sqrt{1 - a}$ B、 $\sqrt{a} - 1$ C、 $\sqrt{1 + a}$ D、 $\sqrt{a} + 1$

查看试题解析
7. 已知 $a = \sqrt{2023 \times 2021}$ ， $b = \sqrt{202 0^{2} + 4 \times 2021}$ ， $c = 2021 \times 2020 - 2019 \times 2021$ ，则 $(a - b) (b - c)$ 的值（）

A、大于零 B、小于零 C、等于零 D、无法确定

查看试题解析
8. 已知数a，b，c在数轴上的位置如图所示，化简： $\sqrt{a^{2}} - | a + c | - \sqrt{{(c - b)}^{2}} - | - b |$ 的结果是（）

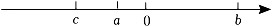A、2c-2b B、-2c C、-2a-2c D、0

查看试题解析
9. 设实数a，b在数轴上对应的位置如图所示，化简 $2 \sqrt{a^{2}} + | a + b |$ 的结果是（）

A、－a＋b B、2a＋b C、3a＋b D、b

查看试题解析
10. 已知 $| a | = 5$ ， $\sqrt{b^{2}} = 7$ ，且 $| a + b | = a + b$ ，则 $a - b$ 的值为（）

A、2或12 B、2或-12 C、-2或12 D、-2或-12

查看试题解析

二、填空题

11. 已知 $\sqrt{8 n}$ 的结果为正整数，则正整数n的最小值为.

查看试题解析
12. 若 $(a - 2)^{2} + | b + 3 | + \sqrt{c - 1} = 0$ ，则 $6 a + 2 b - c =$ .

查看试题解析
13. 将 $\sqrt{32}$ 化成最简二次根式为．

查看试题解析
14. 若 $\sqrt{{(1 - a)}^{2}} = a - 1$ ，则a的取值范围是．

查看试题解析
15. 化简： $\sqrt{(π - 3)^{2}}$ = ．

查看试题解析

三、解答题

16. 实数a、b、c在数轴上的对应点位置如图所示，化简： $\sqrt{(- c)^{2}} + | a - b | + \sqrt[3]{(a + b)^{3}}$ -|b-c|

查看试题解析
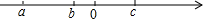17. 实数a，b，c在数轴上如图所示，化简：（ $\sqrt{c}$ ）²﹣ $\sqrt{(a + b)^{2}}$ +|b﹣c|+ $\sqrt{(c - a)^{2}}$ ．

查看试题解析
18. 已知 $y = \sqrt{x - 2} + \sqrt{2 - x} + \frac{3}{8}$ ，求 $\sqrt{x y}$ 的值．

查看试题解析

四、综合题

19.

(1)、已知某正数的平方根为 $a + 3$ 和 $2 a - 15$ ，求这个数是多少？

(2)、已知m，n是实数，且 $\sqrt{2 m + 1} + | 3 n - 2 | = 0$ ，求 $m^{2} + n^{2}$ 的平方根.

查看试题解析
20.

(1)、若a是最小的正整数，b是绝对值最小的数， $c = | \sqrt{7} - \sqrt{11} |$ ， $| x + 2 | + \sqrt{y - 3} = 0$ .则a=；b=；c=；x=；y=.

(2)、若a与b互为相反数，c与d互为倒数， $| e | = \sqrt{2}$ ，求代数式 $4 (a + b) + {(- c d)}^{2} - e^{2}$ 的值.

查看试题解析
21. 已知 $\frac{1}{1 \times 2} = 1 - \frac{1}{2} ； \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ； \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4} ⋯$ ，

(1)、观察上式得出规律，则 $\frac{1}{99 \times 100} =$ ， $\frac{1}{n (n + 1)} =$ ．

(2)、若 $\sqrt{a - 1} + \sqrt{a b - 2} = 0 ，求 a 、 b$ 的值．

(3)、由（2）中 $a$ 、 $b$ 的值，求 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)} + \frac{1}{(a + 2) (b + 2)} + ⋯ + \frac{1}{(a + 2014) (b + 2014)}$ 的值．

查看试题解析
22. 在解决数学问题时，我们一般先仔细阅读题干，找出有用信息作为已知条件，然后利用这些信息解决问题，但是有的题目信息比较明显，我们把这样的信息称为显性条件；而有的信息不太明显，需要结合图形、特殊式子成立的条件、实际问题等发现隐含信息作为条件，我们把这样的条件称为隐含条件；所以我们在做题时，要注意发现题目中的隐含条件．
阅读下面的解题过程，体会如何发现隐含条件并回答下面的问题．

(1)、试化简： $\sqrt{{(x - 3)}^{2}} - {(\sqrt{2 - x})}^{2}$

(2)、已知a，b， c为△ABC的三边长，化简： $\sqrt{(a + b + c)^{2}}$ + $\sqrt{(a - b - c)^{2}}$ + ${\sqrt{(b - a - c)}}^{2}$ + $\sqrt{(c - b - a)^{2}}$ ；

(3)、已知a、b满足 $\sqrt{{(2 - a)}^{2}} = a + 3 ， \sqrt{a - b + 1} = a - b + 1$ 求ab的值

查看试题解析
23. 爱动脑筋的小明在做二次根式的化简时，发现一些二次根式的被开方数是二次三项式，而且这些二次三项式正好是完全平方式的结构，于是就可以利用二次根式的性质： $\sqrt{a^{2}} = | a | = {\begin{array}{l} a (a \geq 0) ， \\ - a (a < 0) \end{array}$ 来进一步化简．
比如： $\sqrt{x^{2} + 2 x + 1} = \sqrt{{(x + 1)}^{2}} = | x + 1 |$ ，
∴当 $x + 1 \geq 0$ 即 $x \geq - 1$ 时，原式 $= x + 1$ ；当 $x + 1 < 0$ 即 $x < - 1$ 时，原式 $= - x - 1$ ．

(1)、仿照上面的例子，请你尝试化简 $\sqrt{m^{2} - m + \frac{1}{4}}$ ．

(2)、判断甲、乙两人在解决问题：“ $a = 9$ ，求 $a + \sqrt{1 - 2 a + a^{2}}$ 的值”时谁的答案正确，并说明理由．
甲的答案：原式 $= a + \sqrt{{(1 - a)}^{2}} = a + (1 - a) = 1$ ；
乙的答案：原式 $= a + \sqrt{{(1 - a)}^{2}} = a + (a - 1) = 2 a - 1 = 2 \times 9 - 1 = 17$ ．

(3)、化简并求值： $| x - 1 | + \sqrt{4 - 4 x + x^{2}}$ ，其中 $x = \sqrt{5}$ ．

查看试题解析

鲁教版（五四学制）2022-2023学年八年级数学下册7.2 二次根式的性质 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年八年级数学下册7.2 二次根式的性质同步测试