鲁教版（五四学制）2022-2023学年八年级数学下册6.3 正方形的性质与判定同步测试

试卷更新日期：2023-01-11 类型：同步测试

进入出卷网下载

一、单选题

1. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把最小的一个正方形按图2的方式放入较大的正方形内，然后把最大的正方形沿BC翻折，记△EHP和正方形ADNM的面积分别为S₁ ， S₂ ．若点N，M，G三点共线，且满足S₁+S₂ =7，则图2中阴影部分的面积为（）

A、 $\frac{49}{5}$ B、 $\frac{51}{5}$ C、 $\frac{54}{5}$ D、 $\frac{56}{5}$

查看试题解析
2. 如图所示，面积为5的正方形 $A B C D$ 的顶点 $A$ 在数轴上，且点 $A$ 表示的数为1，若点 $E$ 在数轴上 $($ 点 $E$ 在点 $A$ 左侧 $)$ ，且 $A D = A E$ ，则点 $E$ 所表示的数为（）

A、 $\sqrt{5}$ B、 $- \sqrt{5}$ C、 $- \sqrt{5} - 1$ D、 $- \sqrt{5} + 1$

查看试题解析
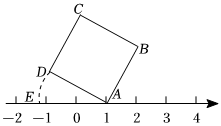3. 如图，正方形ABCD的边长为4，点A的坐标为（-1，1），AB平行于x轴，则点C的坐标为（）

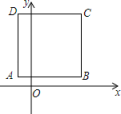A、（3，1） B、（-1，1） C、（3，5） D、（-1，5）

查看试题解析
4. 如图，所有阴影部分的四边形都是正方形，所有三角形都是直角三角形，若正方形A，B，C的面积依次为4，8，6，则正方形D的面积为（）

A、10 B、12 C、16 D、18

查看试题解析
5. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结BG，若大正方形的面积是小正方形面积的5倍，则 $\frac{B G}{B E}$ 的值为（）

A、 $\sqrt{5}$ B、3 C、 $\sqrt{13}$ D、4

查看试题解析
6. 如图，大正方形与小正方形的面积之差是50，则阴影部分的面积是（）

A、12.5 B、25 C、50 D、100

查看试题解析
7. 如果一个正方形的周长为 $(2 a + b)$ （其中 $a > 0$ ， $b > 0$ ），则该正方形的面积为（）

A、 $\frac{a^{2}}{4} + \frac{a b}{4} + \frac{b^{2}}{16}$ B、 $\frac{a^{2}}{4} + \frac{b^{2}}{16}$ C、 $4 a^{2} + b^{2}$ D、 $\frac{a^{2} + 4 a b + b^{2}}{4}$

查看试题解析
8. 如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则E点所表示的数为（）

A、 $\sqrt{5}$ B、1+ $\sqrt{5}$ C、 $\frac{2 + \sqrt{5}}{2}$ D、 $\sqrt{5}$ +2

查看试题解析
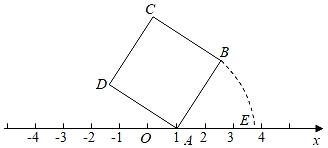9. 三国时期的赵爽利用图1证明了勾股定理，后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中，E，B，F在同一条直线上，四边形ABCD，EFGA，HGDJ都是正方形，若正方形ABCD的面积等于100，△IJD面积等于 $\frac{27}{2}$ ，且已知AH＝2，则△KCD的面积等于（）

A、 $\frac{75}{2}$ B、39 C、 $\frac{77}{2}$ D、52

查看试题解析
10. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积差

查看试题解析

二、填空题

11. 如图，直线l上有三个正方形 $a ， b ， c$ ，若 $a ， b$ 的面积分别为9和25，若抛一颗石子，落在阴影部分的概率为.

查看试题解析
12. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，分别以 $A B 、 B C 、 A C$ 为边向上作正方形 $A G F B$ 、正方形 $B C D E$ 、正方形 $A C M N$ ，点 $E$ 在 $F G$ 上，若 $A C = 2 ， B C = \sqrt{13}$ ，则图中阴影的面积为．

查看试题解析
13. 正方形 $A B C D$ 的对称中心为点 $O$ ，若 $O A = 2$ ，则该正方形的周长为.

查看试题解析
14. 如图，三个正方形围成一个直角三角形，64、400分别为所在正方形的面积，则图中字母M所代表的正方形面积是.

查看试题解析
15. 七巧板是我们祖先的一项卓越创造，被西方人誉为“东方魔板” $.$ 小林将图1的一副七巧板拼成图2的“衣服” $($ 阴影部分 $)$ ，并将它放入方格图中，方格图中的小正方形边长为1，则这件“衣服”的周长为 $(\sqrt{2}$ 取1.4）.

查看试题解析

三、解答题

16. 如图，正方形 $M N B C$ 内有一点A ，以 $A B$ ， $A C$ 为边向 $△ A B C$ 形外作正方形 $A B R T$ 和正方形 $A C P Q$ ，连接 $R M$ ， $B P$ .求证： $B P ∥ R M$ .

查看试题解析

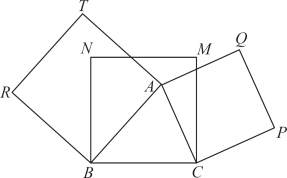17. 党的二十大报告指出大自然是人类赖以生存发展的基本条件……垃圾分类、节能减排、废物再利用等必须从我们身边小事做起.为了充分利用四边形余料，小明设计了不同的方案裁剪正方形，裁剪方案与数据如下表：

方案设计	方案1	方案2
裁剪方案示意图
说明	图中的正方形 $E F B G$ 和正方形 $M N P Q$ 四个顶点都在原四边形的边上
测量数据	$A D = 3 d m$ ， $A B = 9 d m$ ， $C B = 12 d m$ ， $∠ A = ∠ B = 90 °$
任务1：探寻边长关系	填空： $C D =$ ▲ dm； $\frac{P N}{B N}$ = ▲
任务2：比较面积大小	计算或推理：比较正方形 $E F B G$ 和正方形 $M N P Q$ 边长的大小
任务3：应用实践	若在四边形 $A D Q P$ 余料上再截取一个最大正方形，正方形的边长为 ▲

查看试题解析

18. 如图， $E 、 F$ 是正方形 $A B C D$ 的对角线 $B D$ 上的两点，且 $B E = D F$ ，求证： $△ A B E ≅ △ C D F$ ；

查看试题解析

四、综合题

19. 如图

(1)、如图1，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG，BF⊥AG，垂足分别为点E，F.求证： $D E^{2} + B F^{2} = A B^{2}$ ；

(2)、在图1的基础上，若过点C作CH⊥DE，垂足为点H，连接AH，CF，如图2.求证：四边形AFCH为平行四边形.

查看试题解析
20. 如图，四边形 $A B C D$ 是正方形，连接 $A C$ ，将 $△ A B C$ 绕点A逆时针旋转α得到 $△ A E F$ ，连接 $C F$ ， O为 $C F$ 的中点，连接 $O E ， O D$ .

(1)、如图1，当 $α = 45 °$ 时，求证： $O E = O D$ .

(2)、如图2，当 $45 ° < α < 90 °$ 时，（1）中的结论还成立吗？请说明理由.

查看试题解析
21. 在平面直角坐标系中，若点P的坐标为（x，y），则定义：d（x，y）＝|x|+|y|为点P到坐标原点O的“折线距离”.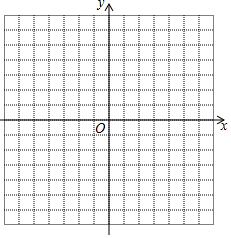

(1)、若已知P（-2，3），则点P到坐标原点O的“折线距离”d（-2，3）＝；

(2)、若点P（x，y）满足2x+y＝0，且点P到坐标原点O的“折线距离”d（x，y）＝6，求出P的坐标；

(3)、若点P到坐标原点O的“折线距离”d（x，y）＝3，试在坐标系内画出所有满足条件的点P构成的图形，并求出该图形的所围成封闭区域的面积.

查看试题解析
22. 如图，点 $E$ 是正方形 $A B C D$ 的边 $A B$ 上的一点，延长 $B C$ 到 $F$ 使 $A E = C F$ ，连接 $D E$ 、 $D F$ .

(1)、能通过旋转 $△ D A E$ 得到 $△ D C F$ 吗？说明理由.

(2)、连接 $E F$ ，过 $D$ 作 $D M$ 垂直 $E F$ 于 $M$ ，交 $B C$ 于 $N$ ，若 $B N = 3$ ， $C N = 2$ ，求 $A E$ 的长.

查看试题解析
23. 如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG．

(1)、如图1，若AD＝2 $\sqrt{3}$ 、DE＝2，当 $∠ A D G ＝ 150 °$ 时，求AG的长；

(2)、如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE之间有何等量关系？并利用图2加以证明．

查看试题解析

鲁教版（五四学制）2022-2023学年八年级数学下册6.3 正方形的性质与判定 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年八年级数学下册6.3 正方形的性质与判定同步测试