鲁教版(五四学制)2022-2023学年八年级数学下册6.2 矩形的性质与判定 同步测试
试卷更新日期:2023-01-11 类型:同步测试
一、单选题
-
1. 以下条件中能判定平行四边形为菱形的是( )A、 B、 C、 D、2. 一个长方形的周长为 , 其中一边长为 , 则与其相邻的一边长为( )A、 B、 C、 D、3. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( )
 A、3 B、 C、 D、64. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( )
A、3 B、 C、 D、64. 如图,在等腰直角三角形中, , 为的中点,为边上一点不与端点重合 , 过点作于点 , 作于点 , 过点作交的延长线于点若 , 则阴影部分的面积为( ) A、12 B、12.5 C、13 D、13.55. 在矩形中,以A为圆心,长为半径画弧,交于F点,以C为圆心,长为半径画弧,交于E点,若 , , 则( )
A、12 B、12.5 C、13 D、13.55. 在矩形中,以A为圆心,长为半径画弧,交于F点,以C为圆心,长为半径画弧,交于E点,若 , , 则( ) A、1 B、 C、 D、6. 如图,在矩形中,两条对角线相交于点O, , , 矩形的面积是( )
A、1 B、 C、 D、6. 如图,在矩形中,两条对角线相交于点O, , , 矩形的面积是( ) A、 B、 C、8 D、127. 下列性质中,菱形具有而矩形不一定具有的是( )A、对边平行且相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直8. 如图,已知长方形纸片ABCD,点E在边AB上,且BE=2,BC=3,将△CBE沿直线CE翻折,使点B落在点G,延长EG交CD于点F处,则线段FG的长为( )
A、 B、 C、8 D、127. 下列性质中,菱形具有而矩形不一定具有的是( )A、对边平行且相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直8. 如图,已知长方形纸片ABCD,点E在边AB上,且BE=2,BC=3,将△CBE沿直线CE翻折,使点B落在点G,延长EG交CD于点F处,则线段FG的长为( ) A、 B、 C、 D、19. 矩形具有而菱形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、邻边相等 D、对角线互相垂直10. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则BC的长为( )
A、 B、 C、 D、19. 矩形具有而菱形不一定具有的性质是( )A、对角线互相平分 B、对角线相等 C、邻边相等 D、对角线互相垂直10. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则BC的长为( )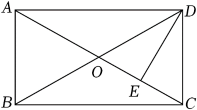 A、 B、6cm C、 D、
A、 B、6cm C、 D、二、填空题
-
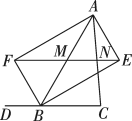
11. 如图,BE,BF分别是与它的邻补角的平分线, , 垂足为点E, , 垂足为点F,EF分别交边AB,AC于点M和N.若 , , 则的长为 .
 12. 如图,在矩形中, , , 矩形绕点逆时针旋转一定角度得矩形 , 若点的对应点落在边上,则的长为.
12. 如图,在矩形中, , , 矩形绕点逆时针旋转一定角度得矩形 , 若点的对应点落在边上,则的长为. 13. 矩形在平面直角坐标系中, , , 将它沿对折,点A落在处,则的坐标是.
13. 矩形在平面直角坐标系中, , , 将它沿对折,点A落在处,则的坐标是.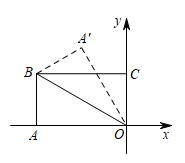 14. 如图,长方形ABCD中,AB=3,AD=4,沿对角线BD折叠,使点A落在点E处,过点E作EF∥CD交BD于点F,连接CF,则CF的长为.
14. 如图,长方形ABCD中,AB=3,AD=4,沿对角线BD折叠,使点A落在点E处,过点E作EF∥CD交BD于点F,连接CF,则CF的长为. 15. 在矩形中,作的平分线交直线于点E,则是度.
15. 在矩形中,作的平分线交直线于点E,则是度.三、解答题
-
16. 如图,在△ABC中,∠ABC=45°,AB= , AC=8,BC>6,点E,F分别在BC,AC边上,且AF=CE,求AE+BF的最小值.
 17. 如图,请用两种不同的方法求阴影部分的面积.
17. 如图,请用两种不同的方法求阴影部分的面积. 18. 已知如图,矩形 , 是矩形的对角线,请用尺规在上找一点 , 在上找一点 , 使得四边形为菱形.
18. 已知如图,矩形 , 是矩形的对角线,请用尺规在上找一点 , 在上找一点 , 使得四边形为菱形.
四、综合题
-
19. 如图,在平行四边形中,对角线 , 相交于点 , 且是等边三角形.
 (1)、证明:平行四边形是矩形;(2)、若 , 求矩形的面积.20. 如图,在平行四边形中, , 延长至点E,使 , 连接 .
(1)、证明:平行四边形是矩形;(2)、若 , 求矩形的面积.20. 如图,在平行四边形中, , 延长至点E,使 , 连接 . (1)、求证:四边形是矩形.(2)、连接 , 若 , 求的长.21. 如图,矩形的顶点E,G分别在菱形的边 , 上,顶点F,H在菱形的对角线上.
(1)、求证:四边形是矩形.(2)、连接 , 若 , 求的长.21. 如图,矩形的顶点E,G分别在菱形的边 , 上,顶点F,H在菱形的对角线上. (1)、求证:;(2)、若E为中点, , 求菱形的周长.22. 如图,一个长方形运动场被分割成 , , , , 共5个区,区是边为米的正方形,区是边长为米的正方形.
(1)、求证:;(2)、若E为中点, , 求菱形的周长.22. 如图,一个长方形运动场被分割成 , , , , 共5个区,区是边为米的正方形,区是边长为米的正方形. (1)、 区相邻两边的长度分别为 米,米.(用含 , 的代数式表示)(2)、如果米,米,求整个长方形运动场的面积.23. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D.
(1)、 区相邻两边的长度分别为 米,米.(用含 , 的代数式表示)(2)、如果米,米,求整个长方形运动场的面积.23. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D. (1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.
(1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.