鲁教版（五四学制）2022-2023学年八年级数学下册6.1 菱形的性质与判定 同步测试
试卷更新日期：2023-01-11 类型：同步测试
一、单选题
-
1. 如图1，在菱形ABCD中，对角线AC、BD相交于O，要在对角线BD上找两点M、N，使得四边形AMCN是菱形，现有图2中的甲、乙两种方案，则正确的方案是（ ）
A、只有甲 B、只有乙 C、甲和乙 D、甲乙都不是2. 如图，菱形中， ， 于 ， 交对角线于 ， 过作于 ． 若的周长为 ， 则菱形的面积为（ ）
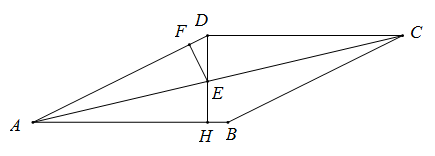A、 B、 C、 D、3. 如图，在平面直角坐标系中，若菱形的顶点A、B的坐标分别为 ， 点D在y轴上，则点C的坐标是（ ）
A、 B、 C、 D、4. 如图，在四边形ABCD中，对角线AC、BD相交于点O，OA=OC，请你添加一个条件，使四边形ABCD是平行四边形，你添加的条件是（ ）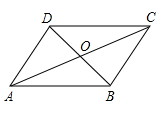
A、AC=BD B、OA=OB C、OA=AD D、OB=0D5. 如图，菱形ABCD的对角线AC、BD相交于点O，BD＝6，AC＝8，E是CD的中点，则OE的长是（ ）
A、2.5 B、3 C、4 D、56. 如图，周长为24的菱形中， ， 点E，F分别是边上的动点，点P为对角线上一动点，则线段的最小值为（ ）
A、 B、 C、 D、7. 如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（ ）
A、40cm B、30cm C、20cm D、10cm8. 菱形中，对角线与的长分别为6和8，则该菱形的周长为（ ）A、 B、20 C、 D、409. 如图，在四边形ABCD中， ， ， 对角线AC，BD交于点O，AC平分 ， 过点C作交AB的延长线与点E，连接OE．嘉嘉说：“四边形ABCD是菱形．”
琪琪说：“ ． ”
对于他俩的说法，正确的是（ ）
A、嘉嘉正确，琪琪错误 B、嘉嘉错误，琪琪正确 C、他俩都正确 D、他俩都错误10. 如图，已知菱形的对角线AC；BD交于点O，E为CD的中点，若 ， 则菱形的周长为（ ）．
A、18 B、48 C、24 D、12二、填空题
-
11. 如图，菱形ABCD中，对角线AC、BD相交于点O，点E为AC上一点，连接DE，AB＝CE＝5AE，BD＝8，则DE的长为 ．
12. 若一个菱形的两条对角线长分别为10和24，则这个菱形的边长是 ．13. 如图，在菱形中，是上一点，连接交对角线于点 ， 连接 ， 若 ， 则°．
14. 如图，点E是菱形的边上一点，且 ， 则 ．
15. 如图，要使平行四边形ABCD为菱形，还需添加的一个条件是 ． （写出一个即可）．
三、解答题
-
16. 如图，在四边形ABCD中， ， 对角线BD垂直平分对角线AC；垂足为点O．求证：四边形是菱形．
17. 已知四边形ABCD，// ， AD=DC=10，DB平分∠ADC，BD=12，求四边形ABCD的面积．
18. 如图，菱形的对角线相交于点O，垂直平分 ， 垂足为点E，求的大小．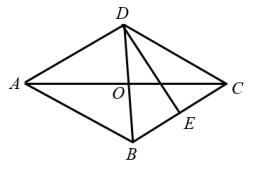
四、综合题
-
19. 在四边形ABCD中，ADBC，AD＝BC，BD平分∠ABC．
(1)、如图1，求证：四边形ABCD是菱形；(2)、如图2，连接AC，过点D作DE⊥BD交BC延长线于点E，在不添加任何辅助线的情况下，请直接写出图中所有与CDE面积相等的三角形（CDE除外）．20. 如图，在平行四边形中， ， 以点为圆心，长为半径画弧交于点 ， 分别以点 ， 为圆心，大于的长为半径作弧，两弧交于点 ， 作射线交于点 ， 交于点 ．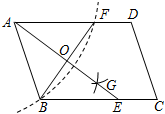
(1)、求证：是等腰三角形；(2)、若 ， ， 求的长．21. 如图，在中，点D，点E分别是边AC，AB的中点，点F在线段DE上，交BC于点G．
(1)、证明：四边形EFGB是菱形；(2)、若 ， 求DF的长度．
