鲁教版（五四学制）2022-2023学年七年级数学下册8.5 平行线的性质定理同步测试

试卷更新日期：2023-01-11 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，AB∥EF，∠ABC＝80°，∠CDF＝135°，则∠BCD的度数为（）

A、30° B、35° C、55° D、80°

查看试题解析
2. 如图，已知 $A B ∥ C D ， B C$ 平分 $∠ A C D ， ∠ B = 35 °$ ， $E$ 是 $C A$ 延长线上一点，则 $∠ B A E$ 的度数是（）

A、 $35 °$ B、 $60 °$ C、 $65 °$ D、 $70 °$

查看试题解析
3. 如图，直线 $a / / b$ ，等边 $△ A B C$ 的顶点C在直线b上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、100° B、110° C、120° D、130°

查看试题解析
4. 如图， $∠ A B C$ 和 $∠ A C B$ 的平分线交于点 $F$ ，过点 $F$ 作 $E G / / B C$ 分别交 $A B$ ， $A C$ 于点 $E$ ， $G$ ，若 $B E = 6$ ， $C G = 10$ ，则线段 $E G$ 的长为（）

A、16 B、17 C、18 D、19

查看试题解析
5. 如图，把长方形 $A B C D$ 沿 $E F$ 对折后使两部分重合，若 $∠ 1 = 40 °$ ，则 $∠ A E F =$ （　　）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
6. 如图在 $△ A B C$ 中， $B F$ 、 $C F$ 是角平分线， $D E ∥ B C$ ，分别交 $A B$ 、 $A C$ 于点D、E， $D E$ 经过点F．结论：① $△ B D F$ 和 $△ C E F$ 都是等腰三角形；② $D E = B D + C E$ ；③ $△ A D E$ 的周长 $= A B + A C$ ；④ $B F = C F$ ．其中正确的是（　　）

A、①② B、②③ C、①②③ D、①②③④

查看试题解析
7. 如图，在△ABC中，∠A=90°，BE，CD分别平分∠ABC和∠ACB，且相交于F， $E G ∥ B C$ ， $C G ⊥ E G$ 于点G，则下列结论 ①∠CEG = 2∠DCA；②CA平分∠BCG；③∠ADC =∠GCD；④∠DFB= $\frac{1}{2}$ ∠A；⑤∠DFE=135°，其中正确的结论是（）

A、①②③ B、①③④ C、①③④⑤ D、①②③④

查看试题解析
8. 如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，AB＝5，BD＝1，则CF的长度为（）

A、2 B、2.5 C、4 D、5

查看试题解析
9. 如图，点A、D、C、E在同一条直线上， $A B ∥ E F ， A B = E F ， ∠ B = ∠ F ， A E = 10$ ， $A C = 6$ ，则 $C D$ 的长为（　　）

A、 $3.5$ B、 $2$ C、 $2.5$ D、 $3$

查看试题解析

二、填空题

10. 如图，△ABC≌△DEC，若∠D＝30°，且CD∥AB，则∠B的度数是 °.

查看试题解析
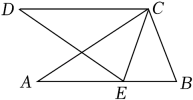11. 如图，在Rt△ABC中，∠A=90°，∠B=30°，CD平分∠ACB交AB于点D，DE∥BC，交AC于点E，若BC=9，则AE的长为．

查看试题解析
12. 如图，∠ABC＝∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC，内角∠ABC，外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有 .

查看试题解析
13. 如图，已知 $A B ∥ C F$ ， E为 $D F$ 的中点，若 $A B = 8 c m$ ， $C F = 5 c m$ ，则 $B D =$ $c m$ ．

查看试题解析
14. 阅读材料：在直角三角形中，斜边和两条直角边满足定理：两条直角边的平方和，等于斜边的平方，因此如果已知两条边的长，根据定理就能求出第三边的长，例如：在 $R t △ A B C$ 中，已知 $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ，由定理得 $A C^{2} + B C^{2} = A B^{2}$ ，代入数据计算求得 $A B = 5$ ．
请结合上述材料和已学几何知识解答以下问题：
已知：如图， $∠ C = 90 °$ ， $A B ∥ C D$ ， $A B = 5$ ， $C D = 11$ ， $A C = 8$ ，点 $E$ 是 $B D$ 的中点，那么 $A E$ 的长为．

查看试题解析

三、解答题

15. 如图， $△ ABC$ 中， $AB = 5$ ， $AC = 6$ ， $∠ ABC$ 与 $∠ ACB$ 的平分线交于点 $I$ ，过 $I$ 做 $DE / / BC$ 分别交 $AB$ ， $AC$ 于点 $D$ ， $E .$ 求 $△ ADE$ 的周长.请补全以下的解答过程.

解： $∵ BI$ 平分 $∠ ABC ($ 已知 $)$ ，

$∴ ∠ 1 = ∠ 2 ($ 角平分线的定义 $)$ ，

又 $∵ DE / / BC ($ 已知 $)$ ，

$∴ ∠ 2 =$ ▲ $($ $)$ ，

$∴ ∠ 1 =$ ▲ ，

$∴ DI =$ ▲ $($ $) .$

同理可得： $EI =$ ▲ .

$∴ △ ADE$ 的周长 $= AD + DE + AE = AD + DI + EI + AE = AD + DB + EC + AE$

$=$ ▲ $+$ ▲ $= 5 + 6 = 11$ .

查看试题解析
16. 如图，已知点 $B ， F ， E ， C$ 在同一条直线上， $A B ∥ C D$ 且 $A B = C D$ ， $∠ A = ∠ D$ .求证： $C E = B F$ .

查看试题解析
17. 如图，AB∥CD，AE⊥BD，CF⊥BD，垂足分别是E、F，且BF=DE，求证：AE=CF

查看试题解析

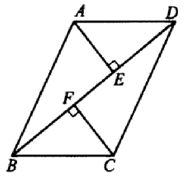
四、综合题

18. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ 分别在 $A B$ ， $A C$ 上，点 $G$ ， $F$ 在 $C B$ 上，连接 $E D$ ， $E F$ ， $G D$ . $∠ 1 + ∠ 2 = 180 °$ ， $∠ B = ∠ 3$ .

(1)、求证： $D E ∥ B C$ ；

(2)、若 $∠ C = 76 °$ ， $∠ A E D = 2 ∠ 3$ ，求 $∠ C E F$ 的度数.

查看试题解析
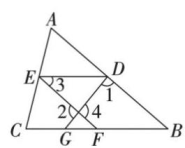19. 如图，△ABC中，已知AB＝AC，BC平分∠ABD.

(1)、求证： $A C ∥ B D$ ；

(2)、若∠A＝100°，求∠1的度数.

查看试题解析
20.

(1)、如图1，在△ABC中，BD平分∠ABC，CD平分∠ACB.过D作EF $∥$ BC交AB于E，交AC于F，请说明EF＝BE＋CF的理由.

(2)、如图2，BD平分∠ABC，CD是△ABC中∠ACB的外角平分线，若仍然过点D作EF $∥$ BC交AB于E，交AC于F，第（1）题的结论还成立吗？如果成立，请说明理由；如果不成立，你能否找到EF与BE、CF之间类似的数量关系？

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ， $∠ 1 = ∠ 2$ ， $D B = D C$ .

(1)、求证： $Δ A B D ≅ Δ E D C$ ；

(2)、若 $∠ A = 135^{0}$ ， $∠ B D C = 30^{0}$ ，求 $∠ B C E$ 的度数．

查看试题解析
22. 在四边形 $A B C D$ 中， $Δ O A B$ 和 $Δ O C D$ 有公共顶点O，且 $Δ O A B ≌ Δ O C D$ .

(1)、如图1，O是边 $B C$ 上的一点.若 $A D ∥ B C$ .求证： $A O = D O$ .

(2)、如图1，O是边 $B C$ 上的一点.若 $∠ A O D = 80 °$ ，连接 $A C ， B D$ ，交点为E，求 $∠ D E C$ 的度数.

(3)、如图2，B、O、C三点不在一条线上，且 $∠ A O B = 90 °$ ，满足 $A D^{2} + B C^{2} = 50 ， A O = 3$ ，求 $Δ O A B$ 的面积.

查看试题解析

鲁教版（五四学制）2022-2023学年七年级数学下册8.5 平行线的性质定理 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

鲁教版（五四学制）2022-2023学年七年级数学下册8.5 平行线的性质定理同步测试