鲁教版(五四学制)2022-2023学年七年级数学下册8.4 平行线的判定定理 同步测试
试卷更新日期:2023-01-11 类型:同步测试
一、单选题
-
1. 如图, , 下列推理正确的是( )
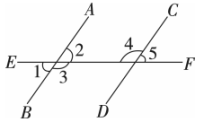
①若 , 则;②若 , 则;③若 , 则;④若 , 则.
A、①② B、②④ C、②③④ D、②③2. 如图,在中, , , , 则射线 与 ( ) A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交3. 如图,过直线外一点作已知直线的平行线,其依据是( )
A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交3. 如图,过直线外一点作已知直线的平行线,其依据是( ) A、同旁内角互补,两直线平行 B、内错角相等,两直线平行 C、两点确定一条直线 D、同位角相等,两直线平行4. 下列命题中,是真命题的是( )A、同位角相等 B、同旁内角相等,两直线平行 C、若 , 则 D、对顶角相等5. 如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( )
A、同旁内角互补,两直线平行 B、内错角相等,两直线平行 C、两点确定一条直线 D、同位角相等,两直线平行4. 下列命题中,是真命题的是( )A、同位角相等 B、同旁内角相等,两直线平行 C、若 , 则 D、对顶角相等5. 如图,点E在AB的延长线上,下列条件中能够判断AD∥BC的是( ) A、∠1=∠3 B、∠C=∠CBE C、∠C+∠ABC=180° D、∠2=∠46. 如图,下列条件中,一定能判断的是( )
A、∠1=∠3 B、∠C=∠CBE C、∠C+∠ABC=180° D、∠2=∠46. 如图,下列条件中,一定能判断的是( )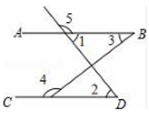 A、 B、 C、 D、7. 下列命题:(1)无限循环小数是无理数;(2)绝对值等于它本身的数是非负数;(3)垂直于同一直线的两条直线互相平行;(4)有两边和其中一边的对角对应相等的两个三角形全等;(5)面积相等的两个三角形全等,是假命题的有( )A、1个 B、2个 C、3个 D、4个8. 如图,下列判断中正确的是( )
A、 B、 C、 D、7. 下列命题:(1)无限循环小数是无理数;(2)绝对值等于它本身的数是非负数;(3)垂直于同一直线的两条直线互相平行;(4)有两边和其中一边的对角对应相等的两个三角形全等;(5)面积相等的两个三角形全等,是假命题的有( )A、1个 B、2个 C、3个 D、4个8. 如图,下列判断中正确的是( )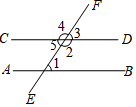 A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么9. 如图,下列条件不能判定的是( )
A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么9. 如图,下列条件不能判定的是( ) A、 B、 C、 D、10. 如图, , , 平分 , 平分 , 则( )
A、 B、 C、 D、10. 如图, , , 平分 , 平分 , 则( )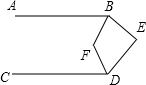 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, , 若 , , 则∠E= .
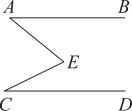 12. 如图所示,用直尺和三角尺作直线AB∥CD,这种作法的依据是.
12. 如图所示,用直尺和三角尺作直线AB∥CD,这种作法的依据是. 13. 如图, , 平分 , 平分 , 可得;平分 , 平分 , 可得设 , , 依次平分下去,则
13. 如图, , 平分 , 平分 , 可得;平分 , 平分 , 可得设 , , 依次平分下去,则 14. 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 .
14. 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件有 . 15. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)
15. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)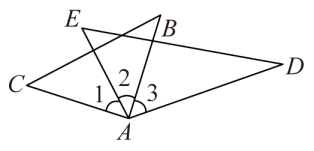
三、解答题
-
16. 如图,C为∠AOB平分线上一点,点D在射线OA上,且OD=CD.
求证:CD∥OB.
 17. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
17. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.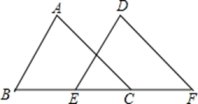 18. 如图,AF=DB,BC=EF,AC=ED,求证:CB∥EF.
18. 如图,AF=DB,BC=EF,AC=ED,求证:CB∥EF.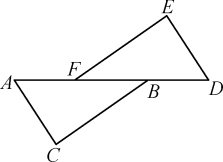
四、综合题
-
19. 如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得EF=ED,连CF.
 (1)、求证:CF∥AB(2)、若∠ABC=50°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.20. 如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,F为AC延长线上的一点,连接DF.
(1)、求证:CF∥AB(2)、若∠ABC=50°,连接BE,BE平分∠ABC,AC平分∠BCF,求∠A的度数.20. 如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,F为AC延长线上的一点,连接DF. (1)、求∠CBE的度数.(2)、若∠F=27°,求证:BEDF.
(1)、求∠CBE的度数.(2)、若∠F=27°,求证:BEDF.


