2022-2023学年浙教版数学七年级下册3.3多项式的乘法 同步练习
试卷更新日期:2023-01-11 类型:同步测试
一、单选题
-
1. 若 , 则的值为( )A、2 B、-2 C、5 D、-52. 如(x+m)与(x+4)的乘积中不含x的一次项,则m的值为( )A、﹣1 B、4 C、0 D、-43. 如图所示的正方形和长方形卡片各有若干张,若要拼成一个长为 ,宽为 的长方形,则需要 类, 类, 类卡片各( )张.


 A、2,3,2 B、2,4,2 C、2,5,2 D、2,5,44. 若(x+2)(2x﹣n)=2x2+mx﹣2,则m+n=( )A、4 B、6 C、2 D、﹣45. 若x是不为0的有理数,已知M=(x2+2x+1)(x2﹣2x+1),N=(x2+x+1)(x2﹣x+1),则M与N的大小是( )A、M>N B、M<N C、M=N D、无法确定6. 若 ,则下列结论正确的是( )A、 B、 C、 D、7. 已知 ,其中☆代表一个常数,则☆的值为( )A、1 B、2 C、3 D、48. 如图是一栋楼房的平面图,下列式子中不能表示它的面积的是( )
A、2,3,2 B、2,4,2 C、2,5,2 D、2,5,44. 若(x+2)(2x﹣n)=2x2+mx﹣2,则m+n=( )A、4 B、6 C、2 D、﹣45. 若x是不为0的有理数,已知M=(x2+2x+1)(x2﹣2x+1),N=(x2+x+1)(x2﹣x+1),则M与N的大小是( )A、M>N B、M<N C、M=N D、无法确定6. 若 ,则下列结论正确的是( )A、 B、 C、 D、7. 已知 ,其中☆代表一个常数,则☆的值为( )A、1 B、2 C、3 D、48. 如图是一栋楼房的平面图,下列式子中不能表示它的面积的是( )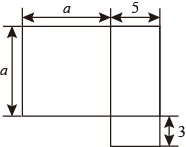 A、 B、(a+5)(a+3)-3a C、a(a+5)+15 D、9. 若的运算结果中,的系数为 , 则a的值是( )A、8 B、 C、4 D、10. 已知 的乘积中不含 项和 项,则a,b的值为( )A、 B、 C、 D、
A、 B、(a+5)(a+3)-3a C、a(a+5)+15 D、9. 若的运算结果中,的系数为 , 则a的值是( )A、8 B、 C、4 D、10. 已知 的乘积中不含 项和 项,则a,b的值为( )A、 B、 C、 D、二、填空题
-
11. 一个长方体的长、宽、高分别是(3x-4)米,(2x+1)米和(x-1)米,则这个长方体的体积是.12. 小轩计算一道整式乘法的题: , 由于小轩将第一个多项式中的“”抄成“”,得到的结果为 .(1)、;(2)、这道题的正确结果是 .13. 若三角形的一边长为2a+4,这边上的高为2a-3,则此三角形的面积为.14. 我们规定一种运算: =ad﹣bc,例如 =3×6﹣4×5=﹣2.按照这种运算规定,已知 =0,则 .15. (x3+3x2+4x-1)(x2-2x+3)的展开式中,x4的系数是
16. 如图,现有A,C两类正方形卡片和B类长方形卡片各若干张,用它们可以拼成一些新的长方形.如果要拼成一个长为(3a+b),宽为(a+2b)的长方形,那么需要B类长方形卡片张.
三、综合题
-
17. 已知(x3+mx+n)(x2﹣3x+1)展开后的结果中不含x3和x2项.(1)、求m、n的值;(2)、求(m+n)(m2﹣mn+n2)的值.18. 如图,长为40,宽为的大长方形被分割为9小块,除阴影 , 两个长方形外,其余7块是形状、大小完全相同的小长方形,其较短一边长为 .
 (1)、分别用含 , 的代数式表示阴影 , 两个长方形的长和宽;(2)、分别用含 , 的代数式表示阴影 , 两个长方形的面积.19. 芳芳计算一道整式乘法的题:(2x+m)(5x﹣4),由于芳芳抄错了第一个多项式中m前面的符号,把“+”写成“﹣”,得到的结果为10x2﹣33x+20.(1)、求m的值;(2)、计算这道整式乘法的正确结果.20. 你能化简 (a﹣1)(a99+a98+a97+…+a2+a+1)吗?
(1)、分别用含 , 的代数式表示阴影 , 两个长方形的长和宽;(2)、分别用含 , 的代数式表示阴影 , 两个长方形的面积.19. 芳芳计算一道整式乘法的题:(2x+m)(5x﹣4),由于芳芳抄错了第一个多项式中m前面的符号,把“+”写成“﹣”,得到的结果为10x2﹣33x+20.(1)、求m的值;(2)、计算这道整式乘法的正确结果.20. 你能化简 (a﹣1)(a99+a98+a97+…+a2+a+1)吗?我们不妨先从简单情况入手,发现规律,归纳结论.
(1)、先填空:(a﹣1)(a+1)=;(a﹣1)(a2+a+1)=;(a﹣1)(a3+a2+a+1)=;由此猜想:(a﹣1)(a99+a98+a97+…+a2+a+1)=
(2)、利用这个结论,你能解决下面两个问题吗?①求 2199+2198+2197+…+22+2+1 的值;
②若 a5+a4+a3+a2+a+1=0,则a6等于多少?