重庆市三峡名校联盟2022-2023学年高一上学期数学秋季联考试卷
试卷更新日期:2023-01-11 类型:月考试卷
一、单选题
-
1. 已知命题: , , 则为( )A、 , B、 , C、 , D、 ,2. 已知函数是幂函数,且在上递减,则实数( )A、 B、2或 C、4 D、23. 是第一象限角或第二象限角,则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 下列散点图中,估计有可能用函数来模拟的是( ).A、
 B、
B、 C、
C、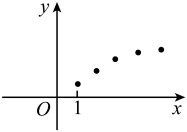 D、
D、 5. 设 , 则( )A、 B、 C、 D、6. 已知函数 , 则( )A、是偶函数,且在是单调递增 B、是奇函数,且在是单调递增 C、是偶函数,且在是单调递减 D、是奇函数,且在是单调递减7. 若为奇函数,且是的一个零点,则一定是下列哪个函数的零点( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设 , 用表示不超过的最大整数,则称为高斯函数,例如: , 已知函数 , 则函数的值域为( )A、 B、 C、 D、
5. 设 , 则( )A、 B、 C、 D、6. 已知函数 , 则( )A、是偶函数,且在是单调递增 B、是奇函数,且在是单调递增 C、是偶函数,且在是单调递减 D、是奇函数,且在是单调递减7. 若为奇函数,且是的一个零点,则一定是下列哪个函数的零点( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设 , 用表示不超过的最大整数,则称为高斯函数,例如: , 已知函数 , 则函数的值域为( )A、 B、 C、 D、二、多选题
-
9. 下列函数中,定义域为的函数是( )A、 B、 C、 D、10. 下列说法正确的是( )A、若 , 则 B、若 , , 则 C、若 , , 则 D、若 , 则11. 已知函数 , 则( )A、 B、若 , 则或 C、的解集为 D、 , 则12. 已知 , 则下列说法正确的是( )A、 B、 C、 D、
三、填空题
-
13. 请写出同时满足下列两个条件的函数.
(1)在定义域内单调递增,(2)14. 求的值为.15. 对于正整数 , 函数定义如下:对于实数 , 记方程的不同实数解的个数为 , 求使得函数的最大值为4的所有正整数的和为.16. 设时钟时针长 , 时间经过小时分钟.①分针转了多少度.(用角度制表示)②时针尖端所走过的弧长为.四、解答题
-
17. 已知函数.(1)、求的最小正周期;(2)、求的最大值和对应的取值;(3)、求在的单调递增区间.18. 在平面直角坐标系中,角的顶点坐标原点,始边为的非负半轴,终边经过点.(1)、求的值;(2)、求的值.19. 在①不等式的解集为 , ②不等式的解集为.这两个条件中任选一个作为已知条件,补充在下面的问题中,并解决该问题.
问题:设
(1)、当时,求;(2)、若“”是“”的充分不必要条件,求的取值范围.20. 已知函数且.(1)、当 , 求函数的单调区间;(2)、若函数的定义域为 , 求的取值范围;(3)、若函数的值域为 , 求的值.21. 习总书记指出:“绿水青山就是金山银山.”某市一乡镇响应号召,因地制宜地将该镇打造成“生态水果特色小镇”.调研过程中发现:某珍稀水果树的单株产量W(单位:kg)与肥料费用(单位:元)满足如下关系: , 其他成本投入(如培育管理等人工费)为(单位:元).已知这种水果的市场售价大约为10元/kg,且供不应求.记该单株水果树获得的利润为(单位:元).(1)、求的函数关系式;(2)、当投入的肥料费用为多少元时,该单株水果树获得的利润最大?最大利润是多少元?22. 定义在上的函数 , 对任意的 , 恒有 , 且时,有(1)、判断的奇偶性并证明;(2)、若 , 且对 , 都有恒成立,求的取值范围;(3)、若 , 函数有三个不同的零点,求的取值范围.