上海市长宁区2022-2023学年高二上学期数学12月月考试卷

试卷更新日期：2023-01-11 类型：月考试卷

进入出卷网下载

一、填空题

1. 抛掷两枚硬币，恰好出现一次正面向上的概率是.

查看试题解析
2. 用斜二测画法画出的水平放置的 $△ A B C$ 的直观图如图，其中 $B^{^{'}} O^{^{'}} = C^{^{'}} O^{^{'}} = 1$ ，若原 $△ A B C$ 的面积为2，则 $A^{'} O^{'} =$ ．

查看试题解析
3. 已知圆锥的侧面积为 $2 π$ ，且它的侧面展开图是一个半圆，则这个圆锥的底面半径是.

查看试题解析
4. 已知事件A与事件B相互独立，若 $P (A) = 0.3$ ， $P (B) = 0.6$ ，则 $P (\bar{A} \cap B) =$ ．

查看试题解析
5. 在四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中的12条棱所在直线中，与直线 $A B_{1}$ 是异面直线的共有条

查看试题解析
6. 为了了解某水库里大概有多少条鱼，先打捞出了1000条鱼，在鱼身上标记一个不会掉落的印记后放回水库，过一段时间后再次捕捞了200条鱼，发现其中5条鱼有印记．则这个水库里大概有条鱼

查看试题解析
7. 正四面体ABCD的各棱长均为2，则点A到平面BCD的距离为．

查看试题解析
8. 下列说法中正确的是．
①一组数据中比中位数大的数和比中位数小的数一样多；
②极差、方差、标准差都是描述一组数据的离散程度的统计量；
③平均数、众数和中位数都是描述一组数据的集中趋势的统计量．

查看试题解析
9. 如图，有一个水平放置的透明无盖的正方体容器，容器高4cm，将一个球放在容器口，再向容器注水，当球面恰好接触水面时，测得水深为3cm．若不计容器的厚度，则球的体积为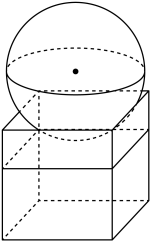 $c m^{3}$

查看试题解析
10. 甲、乙两人进行某项比赛，采用三局两胜模式，假定甲每一局比赛赢的概率都为0.6，则甲最终赢得比赛的概率为．

查看试题解析
11. 从编号分别为1、2、3、4、5的5个大小与质地相同的小球中随机取出3个，则恰有2个小球编号相邻的概率为．

查看试题解析
12. 已知直四棱柱ABCD–A₁B₁C₁D₁的棱长均为2，∠BAD=60°．以 $D_{1}$ 为球心， $\sqrt{5}$ 为半径的球面与侧面BCC₁B₁的交线长为．

查看试题解析

二、单选题

13. 平面 $α$ 与平面 $β$ 相交于直线l，点A、B在平面 $α$ 上，点C在平面 $β$ 上但不在直线l上，直线AB与直线l相交于点D．设A、B、C三点确定的平面为 $γ$ ，则 $β$ 与 $γ$ 的交线是（）

A、直线AC B、直线AB C、直线CD D、直线BC

查看试题解析
14. 掷一颗骰子，设事件 $A$ ：落地时向上的点数是奇数，事件 $B$ ：落地时向上的点数是偶数，事件 $C$ ：落地时向上的点数是 $3$ 的倍数，事件 $D$ ：落地时向上的点数是 $4$ ．则下列每对事件中，不是互斥事件的为（）

A、 $A$ 与 $B$ B、 $B$ 与 $C$ C、 $A$ 与 $D$ D、 $C$ 与 $D$

查看试题解析
15. 某地教育行政部门为了解“双减”政策的落实情况，在某校随机抽取了100名学生，调查他们课后完成作业的时间，根据调查结果绘制如下频率直方图.根据此频率直方图，下列结论中错误的是（）

A、估计该校学生的平均完成作业的时间超过2.7小时 B、所抽取的学生中有25人在2小时至2.5小时之间完成作业 C、该校学生完成作业的时间超过3.5小时的概率估计为20% D、估计该校有一半以上的学生完成作业的时间在2小时至3小时之间

查看试题解析
16. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E为棱BC的中点，F是侧面 $B_{1} B C C_{1}$ 内的动点，若 $A_{1} F / /$ 平面 $A D_{1} E$ ，则点F轨迹的长度为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $2 \sqrt{2}$

查看试题解析

三、解答题

17. 某校共有在校学生200人，为了了解该校学生的体能情况，对该校所有学生进行体能测试，然后采用分层抽样的方法随机抽取了20名学生的成绩，整理得到如下茎叶图：

(1)、求该校女学生人数、样本中女生成绩的极差、25百分数；

(2)、已知全体女生的平均成绩为70，全体男生的平均成绩为72，求该校全体学生的平均成绩．

查看试题解析
18. 如图，在圆柱中，底面直径AB等于母线 $A A_{1}$ ．

(1)、若AB＝2，求圆柱的侧面积；

(2)、设AB与CD是底面互相垂直的两条直径，求异面直线AC与 $A_{1} B$ 所成角的大小．

查看试题解析
19. 如图，已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的高为2，底面ABC是边长为2的正三角形．

(1)、求四棱锥 $A_{1} - B_{1} B C C_{1}$ 的体积；

(2)、若 $A_{1} B = A_{1} C$ ，求证：侧面 $B_{1} B C C_{1}$ 为矩形．

查看试题解析
20. 掷黑、白两枚骰子．

(1)、设事件A为：两枚骰子的点数和为7，事件B为：白色骰子的点数是1．判断事件A和事件B是否独立，并说明理由；

(2)、设事件C为：两枚骰子中至少有一枚的点数是1且两枚骰子点数之和不是7．求事件C的概率．

查看试题解析
21. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为直角梯形， $A D ∥ B C$ ， $A B ⊥ B C$ ， $A B = A D ， B C = 2 A B ， E 、 F$ 分别为棱 $B C 、 B P$ 中点．

(1)、求证：平面 $A E F ∥$ 平面 $D C P$ ；

(2)、若平面 $P B C ⊥$ 平面 $A B C D$ ，直线 $A P$ 与平面 $P B C$ 所成的角为 $4 5^{∘}$ ，且 $C P ⊥ P B$ ，求二面角 $P - A B - D$ 的大小．

查看试题解析