青铜鸣2022-2023学年高二上学期数学联考试卷
试卷更新日期:2023-01-11 类型:月考试卷
一、单选题
-
1. 已知直线上有点 , 则l的倾斜角为( )A、 B、 C、 D、22. 已知等差数列 , 前n项和为 , , 则( ).A、200 B、300 C、500 D、10003. 在四面体中, , 则点B到平面的距离为( )
 A、 B、 C、 D、4. 已知直线l过点 , 且分别交两直线于x轴上方的两点,O点为坐标原点,则面积的最小值为( )A、8 B、9 C、 D、205. 已知初中学过的反比例函数的图象是非标准状况下的双曲线,根据图象的形状及学过的双曲线的相关知识,推断曲线的一个焦点坐标是( )A、 B、 C、 D、6. 已知各项均为正数的等比数列的公比为 , 数列共6项,和为63,前3项和与后3项和的积为392,则( ).A、 B、2 C、 D、2或7. 在平行六面体中, , 且交平面于点M,则( )A、 B、 C、 D、8. 如图,已知抛物线上有不同于原点的三点A,B,C,直线过焦点F, , , 直线交x轴于点 , 则( )
A、 B、 C、 D、4. 已知直线l过点 , 且分别交两直线于x轴上方的两点,O点为坐标原点,则面积的最小值为( )A、8 B、9 C、 D、205. 已知初中学过的反比例函数的图象是非标准状况下的双曲线,根据图象的形状及学过的双曲线的相关知识,推断曲线的一个焦点坐标是( )A、 B、 C、 D、6. 已知各项均为正数的等比数列的公比为 , 数列共6项,和为63,前3项和与后3项和的积为392,则( ).A、 B、2 C、 D、2或7. 在平行六面体中, , 且交平面于点M,则( )A、 B、 C、 D、8. 如图,已知抛物线上有不同于原点的三点A,B,C,直线过焦点F, , , 直线交x轴于点 , 则( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、多选题
-
9. 已知点在内,则下列表述正确的是( )A、 B、直线与圆相交 C、过点的弦长最小值为 D、与相内切10. 在三棱锥中, 四点分别为棱的中点,则以下表述正确的是( )A、若 , 则 B、 C、若 , 则 D、11. 已知数列满足 , 则( )A、 B、 C、 D、的n的最大值为1012. 以下为自然数从小到大依次排成的数阵:
1
2 3
4 5 6 7
8 9 10 11 12 13 14 15
……
第行有个数,则( ).
A、该数阵第行第一个数为 B、该数阵第行所有数的和为 C、该数阵第行最后一个数为 D、若数阵前行总和为 , , 则的最大值为7三、填空题
-
13. 若数列满足 , 且数列单调递减,则的取值范围是 .14. 已知双曲线的左焦点为F,过F且斜率为的直线交两渐近线于x轴上方的不同两点C,D,且 , 则 .15. 台球赛的一种得分战术手段叫做“斯诺克”:在白色本球与目标球之间,设置障碍,使得本球不能直接击打目标球.如图,某场比赛中,某选手被对手做成了一个“斯诺克”,本球需经过边 , 两次反弹后击打目标球N,点M到的距离分别为 , 点N到的距离分别为 , 将M,N看成质点,本球在M点处,若击打成功,则 .
 16. 已知椭圆的左、右顶点分别为A,B,椭圆上有点M, , , 则椭圆的离心率为 .
16. 已知椭圆的左、右顶点分别为A,B,椭圆上有点M, , , 则椭圆的离心率为 .四、解答题
-
17. 已知 , 两圆交于 两点,两圆的一条公切线段 .(1)、求的值;(2)、求点到直线距离的最大值.18. 在长方体中, , M为中点, .
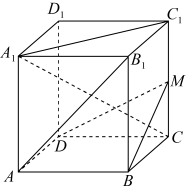 (1)、求异面直线与所成角的余弦值;(2)、 分别为直线上的点,求的最小值.19. 已知抛物线 , O点为坐标原点,过点的直线交抛物线于A,B两点, .
(1)、求异面直线与所成角的余弦值;(2)、 分别为直线上的点,求的最小值.19. 已知抛物线 , O点为坐标原点,过点的直线交抛物线于A,B两点, . (1)、求抛物线的方程;(2)、以点M为圆心的圆与抛物线有四个交点分别为P,Q,S,T,当等腰梯形的一条对角线的斜率为2时,求圆M的半径.
(1)、求抛物线的方程;(2)、以点M为圆心的圆与抛物线有四个交点分别为P,Q,S,T,当等腰梯形的一条对角线的斜率为2时,求圆M的半径.
