2022-2023学年浙教版数学七年级下册3.2单项式的乘法 同步练习
试卷更新日期:2023-01-11 类型:同步测试
一、单选题
-
1. 计算的结果是( )A、 B、 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 如果的结果中不含x的五次项,那么m的值为( )A、1 B、0 C、-1 D、4. 计算:□,□内应填写( )A、-10xy B、 C、+40 D、+40xy5. 已知单项式与的积为 , 那么m-n=( )A、-11 B、5 C、1 D、-16. 已知单项式6am+1bn+1与-4a2m-1b2n-1的积与7a3b6是同类项,则mn的值为( )A、1 B、2 C、3 D、47. 如图是一所楼房的平面图,下列式子中不能表示它的面积的是( )
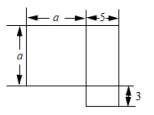 A、a2+5a+15 B、(a+5)(a+3)﹣3a C、a(a+5)+15 D、a(a+3)+a28. 已知(-2x)·(5-3x+mx2-nx3)的结果中不含x3项,则m的值为( )A、1 B、-1 C、- D、09. 与的关系是( )A、相等 B、互为相反数 C、前式是后式的倍 D、以上结论都不对10. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
A、a2+5a+15 B、(a+5)(a+3)﹣3a C、a(a+5)+15 D、a(a+3)+a28. 已知(-2x)·(5-3x+mx2-nx3)的结果中不含x3项,则m的值为( )A、1 B、-1 C、- D、09. 与的关系是( )A、相等 B、互为相反数 C、前式是后式的倍 D、以上结论都不对10. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )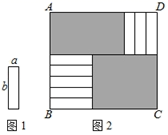 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 若 与 的乘积中不含 的一次项,则 .13. 已知计算xn·(xn+x2-1)的结果是一个六次多项式,则n=.14. 若单项式与是同类项,那么这两个单项式的积是 .15. 已知单项式 与 的积为 ,那么m-n= .16. 如果长方体的长为3a﹣4,宽为2a,高为2a,则它的体积是.
三、计算题
-
17. 计算: .
四、解答题
-
18. 阅读下列文字,并解决问题。
已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到满足x2y=3的x,y的可能值较多,不可以逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)
=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y,
将x2y=3代入
原式=2×33-6×32-8×3=-24.
请你用上述方法解决下面问题:
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
19. 如图,一长方形地块用来建造住宅、广场、商厦,求这块地的面积.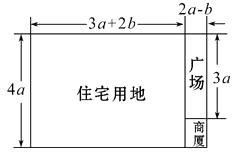
五、综合题
-
20. 王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
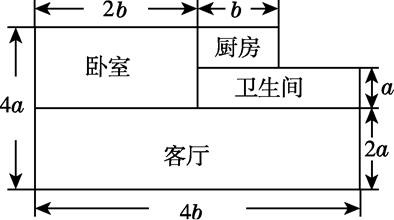 (1)、木地板和地砖分别需要多少平方米?(2)、如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
(1)、木地板和地砖分别需要多少平方米?(2)、如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
-