河北省沧州市海兴县2023届高三上学期数学12月调研试卷
试卷更新日期:2023-01-11 类型:月考试卷
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知复数z满足: , 则( )A、 B、 C、1 D、3. 某高校甲、乙两位同学大学四年选修课程的考试成绩等级(选修课的成绩等级分为1,2,3,4,5,共五个等级)的条形图如图所示,则甲成绩等级的中位数与乙成绩等级的众数分别是( )

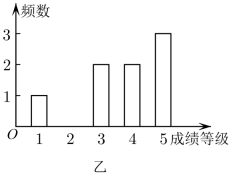 A、3,5 B、3,3 C、3.5,5 D、3.5,44. 若x,y,z为非零实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知函数( , , )的部分图象如图所示,则下列四个结论中正确的是( )
A、3,5 B、3,3 C、3.5,5 D、3.5,44. 若x,y,z为非零实数,则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 已知函数( , , )的部分图象如图所示,则下列四个结论中正确的是( ) A、若 , 则函数f(x)的值域为 B、点是函数f(x)图象的一个对称中心 C、函数f(x)在区间上是增函数 D、函数f(x)的图象可以由函数的图象向右平移个单位长度得到6. 已知点 , , , , 则向量与夹角的余弦值为( )A、 B、 C、 D、7. 满足 , 则实数a的取值范围为( )A、 B、 C、 D、8. 已知函数 , 若时 , 则实数a的取值范围为( )A、 B、 C、 D、
A、若 , 则函数f(x)的值域为 B、点是函数f(x)图象的一个对称中心 C、函数f(x)在区间上是增函数 D、函数f(x)的图象可以由函数的图象向右平移个单位长度得到6. 已知点 , , , , 则向量与夹角的余弦值为( )A、 B、 C、 D、7. 满足 , 则实数a的取值范围为( )A、 B、 C、 D、8. 已知函数 , 若时 , 则实数a的取值范围为( )A、 B、 C、 D、二、多选题
-
9. 北京天坛圜丘坛的地面由石板铺成,最中间的是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外各圈的石板数依次为 , , , , , 设数列为等差数列,它的前n项和为 , 且 , , 则( )
 A、 B、的公差为9 C、 D、10. 已知函数的零点为 , 则( )A、的值为5 B、的值为4 C、 D、11. 已知双曲线的左、右焦点分别为 , , 左、右顶点分别为 , , P为双曲线的左支上一点,且直线与的斜率之积等于3,则下列说法正确的是( )A、双曲线的离心率为2 B、若 , 且 , 则 C、以线段 , 为直径的两个圆外切 D、若点P在第二象限,则12. 已知正方体的棱长为2,P,Q分别为棱 , 的中点,M为线段BD上的动点,则( )
A、 B、的公差为9 C、 D、10. 已知函数的零点为 , 则( )A、的值为5 B、的值为4 C、 D、11. 已知双曲线的左、右焦点分别为 , , 左、右顶点分别为 , , P为双曲线的左支上一点,且直线与的斜率之积等于3,则下列说法正确的是( )A、双曲线的离心率为2 B、若 , 且 , 则 C、以线段 , 为直径的两个圆外切 D、若点P在第二象限,则12. 已知正方体的棱长为2,P,Q分别为棱 , 的中点,M为线段BD上的动点,则( ) A、 B、 C、三棱锥的体积为定值 D、M为BD的中点时,则二面角的平面角为60°
A、 B、 C、三棱锥的体积为定值 D、M为BD的中点时,则二面角的平面角为60°三、填空题
-
13. 若的展开式中的系数为224,则正实数的值为 .14. 2022年北京冬奥会即将开幕,某校4名学生报名担任志愿者.将这4名志愿者分配到3个比赛场馆,每个比赛场馆至少分配一名志愿者,则所有分配方案共有种.(用数字作答)15. 已知点M的坐标为(2,0),AB是圆O:的一条直径,则 .16. 九连环是我国古代至今广为流传的一种益智游戏,它由九个铁丝圆环相连成串,按一定规则移动圆环的次数,决定解开圆环的个数在某种玩法中,用an表示解下n(n≤9,n∈N*)个圆环所需的最少移动次数,数列{an}满足a1=1,且an= , 则解下n(n为奇数)个环所需的最少移动次数为.(用含n的式子表示)
四、解答题
-
17. 已知等差数列的首项为2,且 , , 成等比数列.数列的前n项和为 , 且.(1)、求与的通项公式;(2)、若 , 求数列的前n项和.18. 设a,b,c分别是 的内角A,B,C的对边, .(1)、求角A的大小;(2)、从下面两个问题中任选一个作答 , 两个都作答则按第一个记分.
①设角A的角平分线交BC边于点D,且 ,求 面积的最小值.
②设点D为BC边上的中点,且 ,求 面积的最大值.
19. 某统计部门依据《中国统计年鉴——2017》提供的数据,对我国1997-2016年的国内生产总值(GDP)进行统计研究,作出了两张散点图:图1表示1997-2016年我国的国内生产总值(GDP),图2表示2007-2016年我国的国内生产总值(GDP).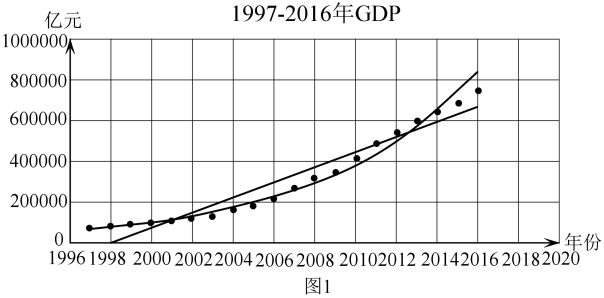
 (1)、用表示第i张图中的年份与GDP的线性相关系数, , 依据散点图的特征分别写出的结果;(2)、分别用线性回归模型和指数回归模型对两张散点图进行回归拟合,分别计算出统计数据——相关指数的数值,部分结果如下表所示:
(1)、用表示第i张图中的年份与GDP的线性相关系数, , 依据散点图的特征分别写出的结果;(2)、分别用线性回归模型和指数回归模型对两张散点图进行回归拟合,分别计算出统计数据——相关指数的数值,部分结果如下表所示:年份
1997-2016
2007-2016
线性回归模型
0.9306
指数回归模型
0.9899
0.978
①将上表中的数据补充完整(结果保留3位小数,直接写在答题卡上);
②若估计2017年的GDP,结合数据说明采用哪张图中的哪种回归模型会更精准一些?若按此回归模型来估计,2020年的GDP能否突破100万亿元?事实上,2020年的GDP刚好突破了100万亿元,估计与事实是否吻合?结合散点图解释说明.
20. 如图,一张边长为4的正方形纸片ABCD,E,F分别是AD,BC的中点,将正方形纸片沿EF对折后竖立在水平的桌面上. (1)、求证:;(2)、若二面角的平面角为45°,K是线段CF(含端点)上一点,问是否存在点K,使得直线AK与平面CDEF所成角的正切值为?若存在,求出CK的长度;若不存在,说明理由.
(1)、求证:;(2)、若二面角的平面角为45°,K是线段CF(含端点)上一点,问是否存在点K,使得直线AK与平面CDEF所成角的正切值为?若存在,求出CK的长度;若不存在,说明理由.