陕西省汉中市宁强县2022-2023学年八年级上学期期末测数学试题

试卷更新日期：2023-01-11 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{9}$ 的值等于（）

A、3 B、 $- 3$ C、 $\pm 3$ D、5

查看试题解析
2. 图中字母所代表的正方形的面积为175的选项为（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（　　　）

A、 $a + 2 a^{2} = 3 a^{3}$ B、 $a^{2} + a^{3} = a^{6}$ C、 $2 a \cdot 3 a = 6 a$ D、 ${(a^{3})}^{2} = a^{6}$

查看试题解析
4. 下列命题中，是真命题的是（）

A、三角形三条高所在直线一定相交于三角形内 B、一个数能被6整除，这个数也能被4整除 C、三角形的三个外角和等于180度 D、平方根等于它本身的数是0

查看试题解析
5. 下列计算正确的是（）

A、 $a^{6} \div a^{3} = a^{2}$ B、 ${(- m)}^{7} \div {(- m)}^{2} = - m^{5}$ C、 ${(3 a^{2} b)}^{2} = 6 a^{4} b^{2}$ D、 ${(a - 2)}^{2} = a^{2} - 4$

查看试题解析
6. 下列条件能够判断两个三角形全等的是（）

A、两个三角形周长相等 B、两个三角形三个内角分别相等 C、两个三角形有两条边和其中一条边上的中线分别相等 D、两个三角形有两条边和一对角分别相等

查看试题解析
7. 根据下列条件不能唯一画出△ABC的是（）

A、AB＝5，BC＝6，AC＝7 B、AB＝5，BC＝6，∠B＝45° C、AB＝5，AC＝4，∠C＝90° D、AB＝3，AC＝4，∠C＝45°

查看试题解析
8. 如图所示，点 $A ， B$ 分别是 $∠ N O F ， ∠ M O F$ 平分线上的点， $A B ⊥ O F$ 于点 $E$ ， $B C ⊥ M N$ 于点 $C$ ， $A D ⊥ M N$ 于点 $D$ ，下列结论错误的是（）

A、 $∠ A O B = 90^{\circ}$ B、 $A D + B C = A B$ C、点 $O$ 是 $C D$ 的中点 D、图中与 $∠ C B O$ 互余的角有两个

查看试题解析

二、填空题

9. $4^{7} \times {(0.25)}^{7} =$ .

查看试题解析
10. 若 $x^{2} = 64$ ，则x的值为.

查看试题解析
11. 一个等腰三角形有一个角为 $8 0^{∘}$ ，则它的顶角度数为

查看试题解析
12. 为了解社会对宁强教育满意程度，某数学学习小组随机电话访问了200名评议代表，并对持有三种意见的人数进行统计，绘制出如图所示统计图，则对宁强教育非常满意的有人.

查看试题解析
13. 如图，长方形 $A B C D$ 中， $A B = 6 ， A D = 12$ ， E为 $B C$ 边上的动点，F为 $C D$ 的中点，连接 $A E ， E F$ ，则 $A E + E F$ 的最小值为

查看试题解析

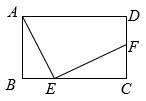
三、解答题

14. 计算：

(1)、 $- {(\frac{5}{12})}^{6} \times {(- 4)}^{5} \times {(2 \frac{2}{5})}^{6} \times 0.2 5^{6}$

(2)、 $a^{5} \cdot (- a)^{3} + (- 2 a^{2})^{4}$

查看试题解析
15. 先化简，再求值： $x (x - 2) - (x + 1) (x - 1)$ ，其中 $x = 10$ .

查看试题解析
16. 分解因式：

(1)、 $2 x^{3} - 8 x$ ；

(2)、 $(x^{2} + 1)^{2} - 4 x^{2}$ .

查看试题解析
17. 已知：如图，AE=CF，AD $∥$ BC，AD=CB，问DF与BE平行吗？为什么？

查看试题解析
18. 已知线段a，h（图），用直尺和圆规作等腰三角形 $A B C$ ，使底边 $B C = a$ ，底边 $B C$ 边上的高线长为h.

查看试题解析
19. 如图，点D、E在 $Δ A B C$ 的 $B C$ 边上， $A D = A E$ ， $A B = A C$ ，求证： $B D = C E$ .

查看试题解析
20. 在 $△ A B C$ 中， $A B = C B$ ， $∠ A B C = 90 °$ ， F为 $A B$ 延长线上一点，点E在 $B C$ 上，且 $A E = C F$ .

(1)、求证： $B E = B F$ ；

(2)、若 $∠ C A E = 30 °$ ，求 $∠ A C F$ 度数.

查看试题解析
21. 如图，某校攀岩墙 $A B$ 的顶部A处安装了一根安全绳 $A C$ ，让它垂到地面时比墙高多出了2米，教练把绳子的下端C拉开8米后，发现其下端刚好接触地面（即 $B C = 8$ 米）， $A B ⊥ B C$ ，求攀岩墙 $A B$ 的高度.

查看试题解析
22. 为了解我县八年级学生期末数学考试情况，在八年级随机抽取了一部分学生的期末数学成绩为样本，分为 A（96～120分）；B（72～95分）；C（60～71分）； D（0～59分）四个等级进行统计，并将统计结果绘制成如下统计图，请你根据统计图解答以下问题.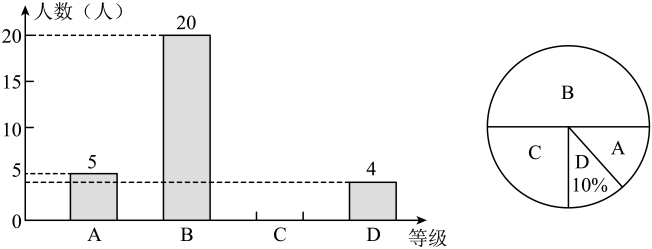

(1)、这次随机抽取的学生共有多少人？

(2)、请补全条形统计图；

(3)、这个学校八年级共有学生1200人，请估计这次八年级学生期末数学考试成绩为B级及以上的学生人数大约有多少？

查看试题解析
23. 在下列网格中，每个小正方形的边长均为1，请按要求画出格点三角形.

(1)、在图1中画出一个等腰 $△ ABC$ .

(2)、在图2中画出一个 $Rt △ ABD$ ，且其三边都不与网格线重合.

查看试题解析
24. 【背景介绍】勾股定理是几何学中的明珠，充满着魅力.
【知识运用】

(1)、如图，铁路上A、B两点（看作直线上的两点）相距40千米，C、D为两个村庄（看作两个点）， $A D ⊥ A B$ ， $B C ⊥ A B$ ，垂足分别为A、B， $A D = 35$ 千米， $B C = 5$ 千米，则两个村庄的距离为米.

(2)、在（1）的背景下，若 $A B = 40$ 千米， $A D = 24$ 千米， $B C = 16$ 千米，现要在 $A B$ 上建造一个供应站P，使得 $P C = P D$ ，请用尺规作图在图中作出P点的位置并求出 $A P$ 的距离.

(3)、【知识迁移】借助上面的思考过程与几何模型，则代数式 $\sqrt{x^{2} + 25} + \sqrt{(9 - x)^{2} + 49}$ （其中 $0 < x < 9$ ）最小值为.

查看试题解析
25.

(1)、如图1， $△ A B C$ 与 $△ A D E$ 均是顶角为 $40 °$ 的等腰三角形， $B C$ 、 $D E$ 分别是底边，求证： $B D = C E$ ；

(2)、如图2， $△ A C B$ 和 $△ D C E$ 均为等边三角形，点A、D、E在同一直线上，连接 $B E$ ．
填空： $∠ A E B$ 的度数为；线段 $B E$ 与 $A D$ 之间的数量关系是．

(3)、拓展探究
如图3， $△ A C B$ 和 $△ D C E$ 均为等腰直角三角形， $∠ A C B = ∠ D C E = 90 °$ ，点A、D、E在同一直线上， $C M$ 为 $△ D C E$ 中 $D E$ 边上的高，连接 $B E$ ．请判断 $∠ A E B$ 的度数及线段 $C M$ 、 $A E$ 、 $B E$ 之间的数量关系，并说明理由．

查看试题解析