江苏省宿迁市泗洪县2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-01-11 类型:期末考试
一、单选题
-
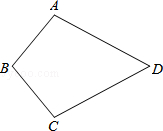
1. 9的算术平方根是( )A、3 B、-3 C、±3 D、812. 下列各数中是无理数的是( )A、 B、 C、 D、3. 下列函数中,是一次函数的是( )A、 B、 C、 D、4. 已知点P(1+m,3)在第二象限,则m的取值范围是( )A、 B、 C、 D、5. 已知 , 是正比例函数 图像上的两点,若 , 则与的大小关系是( )A、 B、 C、 D、不能确定6. 下列长度的三条线段能组成直角三角形的是( )A、 B、 C、32 , 42 , 52 D、4,5,67. 如图,在四边形中,点E在边上, , , , 则的度数为( )
 A、 B、 C、 D、8. 为落实“五育并举”,某校利用课后延时服务时间进行趣味运动,甲同学从跑道A处匀速跑往B处,乙同学从B处匀速跑往A处,两人同时出发,到达各自终点后立即停止运动.设甲同学跑步的时间为x(秒),甲、乙两人之间的距离为y(米),y与x之间的函数关系如图所示,则图中t的值是( )
A、 B、 C、 D、8. 为落实“五育并举”,某校利用课后延时服务时间进行趣味运动,甲同学从跑道A处匀速跑往B处,乙同学从B处匀速跑往A处,两人同时出发,到达各自终点后立即停止运动.设甲同学跑步的时间为x(秒),甲、乙两人之间的距离为y(米),y与x之间的函数关系如图所示,则图中t的值是( ) A、 B、18 C、 D、20
A、 B、18 C、 D、20二、填空题
-
9. 若代数式 在实数范围内有意义,则x的取值范围是。10. 点与点Q关于x轴对称,则点Q的坐标是.11. 小亮的体重为44.85kg,精确到0.1kg得到的近似值为kg.12. 圆面积S与直径d之间的函数表达式为S=.13. 将函数的图象向下平移个单位长度后,得到新图像的函数表达式为.14. 如图,△ABC≌△DEF,BE=5,BF=1,则CF=.
 15. 如图,直线 与直线 交于P ,则方程组 的解是 .
15. 如图,直线 与直线 交于P ,则方程组 的解是 .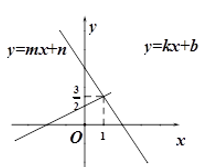 16. 仔细观察图形,以点为圆心的弧线与x轴交于P点,则P点的坐标为.
16. 仔细观察图形,以点为圆心的弧线与x轴交于P点,则P点的坐标为.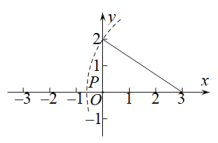 17. 如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是( , 0),则点A的坐标为.
17. 如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是( , 0),则点A的坐标为.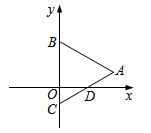 18. 已知过点的直线不经过第一象限.s=a+2b,则s的取值范围是.
18. 已知过点的直线不经过第一象限.s=a+2b,则s的取值范围是.三、解答题
-
19. 计算:.20. 求下列各式中的x:(1)、;(2)、.21. 如图,已知:AB=CB,AD=CD,求证:∠A=∠C.
 22. 已知与成正比例,且当时,.求y与x的函数表达式.23. 已知三点: , , .
22. 已知与成正比例,且当时,.求y与x的函数表达式.23. 已知三点: , , .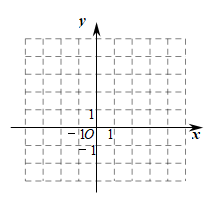 (1)、在所给的平面直角坐标系中画出;(2)、若C点与点关于x轴对称,求直线的函数表达式.24. 如图,在中, , 点D在上, , , 垂足分别为E、F,且.求证:D是的中点.
(1)、在所给的平面直角坐标系中画出;(2)、若C点与点关于x轴对称,求直线的函数表达式.24. 如图,在中, , 点D在上, , , 垂足分别为E、F,且.求证:D是的中点.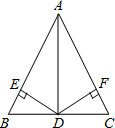 25. 已知:如图,在中,是高,E、F分别是、的中点.
25. 已知:如图,在中,是高,E、F分别是、的中点.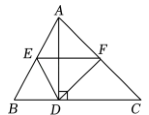 (1)、 , , 求四边形的周长;(2)、与有怎样的位置关系?证明你的结论.26. 如图,已知直线:与直线平行,与x轴交于点A,与y轴交于点B.直线与y轴交于点 , 与x轴交于点D,与直线交于点.
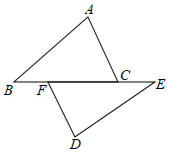
(1)、 , , 求四边形的周长;(2)、与有怎样的位置关系?证明你的结论.26. 如图,已知直线:与直线平行,与x轴交于点A,与y轴交于点B.直线与y轴交于点 , 与x轴交于点D,与直线交于点.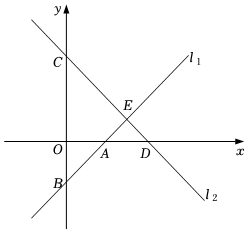 (1)、求直线对应的函数表达式;(2)、求四边形的面积.27. 如图,在长方形纸片ABCD中,AB=CD=5,AD=BC=3.
(1)、求直线对应的函数表达式;(2)、求四边形的面积.27. 如图,在长方形纸片ABCD中,AB=CD=5,AD=BC=3. (1)、尺规作图:在边BC找一点P,使得△ABP沿直线AP折叠时,B点恰好落在边CD上:(写出作法过程,保留作图痕迹,不需证明)(2)、求BP的长.28. 客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,且部分对应关系如表所示.
(1)、尺规作图:在边BC找一点P,使得△ABP沿直线AP折叠时,B点恰好落在边CD上:(写出作法过程,保留作图痕迹,不需证明)(2)、求BP的长.28. 客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,且部分对应关系如表所示.x(kg)
…
30
40
50
…
y(元)
…
4
6
8
…
(1)、求y关于x的函数表达式;(2)、求旅客最多可免费携带行李的质量;(3)、当行李费2≤y≤7(元)时,可携带行李的质量x(kg)的取值范围是.