河南省信阳市淮滨县2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-01-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $(a b)^{2} = a b^{2}$ D、 $(a^{2})^{4} = a^{8}$

查看试题解析
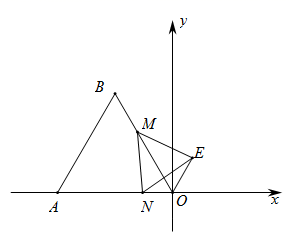
3. 如图，一名工作人员不慎将一块三角形模具打碎成三块，他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具，他带（）去最省事.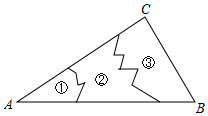

A、① B、② C、③ D、①③

查看试题解析
4. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 10^{- 7}$ B、 $4.6 \times 10^{- 7}$ C、 $4.6 \times 10^{- 6}$ D、 $0.46 \times 10^{- 5}$

查看试题解析
5. 已知 $x = - 2$ 时，分式 $\frac{x - 1}{□}$ 无意义，则“□”可以是（　　）

A、 $2 - x$ B、 $x - 2$ C、 $2 x + 4$ D、 $x + 4$

查看试题解析
6. 在测量一个小口圆形容器的壁厚时，小明用“ $X$ 型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝7厘米，圆形容器的壁厚是（　　）

A、1厘米 B、2厘米 C、5厘米 D、7厘米

查看试题解析
7. 关于x的分式方程 $\frac{m + x}{2 - x} -$ 3＝0有解，则实数m应满足的条件是（）

A、m＝﹣2 B、m≠﹣2 C、m＝2 D、m≠2

查看试题解析
8. 如图，在 $Δ A B C$ 中，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 的长为半径作弧，两弧相交于点M、N，直线 $M N$ 与 $A C$ 、 $B C$ 分别相交于E和D，连接 $A D$ ，若 $A E = 3 c m$ ， $Δ A B C$ 的周长为 $13 c m$ ，则 $Δ A B D$ 的周长是（）

A、 $7 c m$ B、 $10 c m$ C、 $16 c m$ D、 $19 c m$

查看试题解析
9. 如图，点P是∠BAC平分线AD上的一点，AC=9，AB=5，PB=3，则PC的长可能是（）

A、6 B、7 C、8 D、9

查看试题解析
10. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是（）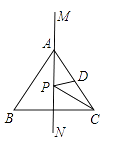

A、30° B、15° C、20° D、35°

查看试题解析

二、填空题

11. 计算： ${(- \frac{1}{4})}^{- 1} + {(- 2)}^{2} \times 201 9^{0} =$ .

查看试题解析
12. 在平面直角坐标系 $x O y$ 中，点 $M (- 4 ， 2)$ 关于x轴对称的点的坐标是.

查看试题解析
13. 正多边形的一个外角等于60，这个多边形的边数是.

查看试题解析
14. 如图，∠MOP=60°，OM=5，动点N从点O出发，以每秒1个单位长度的速度沿射线OP运动.设点N的运动时间为t秒，当△MON是锐角三角形时，t满足的条件.

查看试题解析
15. 定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“和谐分式”.如： $\frac{x + 1}{x - 1} = \frac{x - 1 + 2}{x - 1} = \frac{x - 1}{x - 1} + \frac{2}{x - 1} = 1 + \frac{2}{x - 1}$ ，则 $\frac{x + 1}{x - 1}$ 是“和谐分式”.同时我们也可以将“和谐分式化成一个整式与一个分子为常数的分式的和的形式，如： $\frac{a^{2} - 2 a + 3}{a - 1} = a - 1 + \frac{2}{a - 1}$ ，那么若分式： $\frac{3 x + 6}{x + 1} - \frac{x - 1}{x} \div \frac{x^{2} - 1}{x^{2} + 2 x}$ 的值为整数.则整数x取值为：.

查看试题解析

三、解答题

16.

(1)、因式分解： $a^{2} (a - b) - 4 (a - b)$ ；

(2)、计算： $(1 + a) (1 - a) + a (a - 3)$ ；

查看试题解析
17. 先化简，再求值： $\frac{m^{3} - 2 m^{2}}{m^{2} - 4 m + 4} \div (\frac{9}{m - 3} + m + 3)$ ，其中m是已知两边分别为2和3的三角形的第三边长，且m是整数.

查看试题解析
18. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (4 ， 5)$ ， $B (1 ， 0)$ ， $C (4 ， 0)$ .

( 1 )画出 $△ A B C$ 关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ，并写出点 $A_{1}$ 的坐标；

( 2 )在y轴上求作一点P，使 $△ P A B$ 的周长最小，并写出点P的坐标.

查看试题解析
19. 问题1：如图①，在四边形ABCD中， $∠ B = ∠ C = 90 °$ ， P是BC上一点， $P A = P D$ ， $∠ A P D = 90 °$ .易得 $△ A B P ≌ △ P C D$ .（不需证明）
问题2：如图②，在四边形ABCD中， $∠ B = ∠ C = 45 °$ ， P是BC上一点， $P A = P D$ ， $∠ A P D = 90 °$ .

(1)、求证： $B P = C P$ ；

(2)、若 $B C = 8$ ，求 $△ A B P$ 与 $△ P C D$ 的面积和.

查看试题解析
20. 如图1是一个长为 $4 a$ 、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）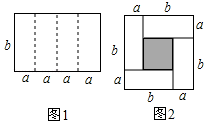

(1)、观察图2请你写出 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的等量关系是；

(2)、根据（1）中的结论，若 $x + y = 5 ， x \cdot y = \frac{9}{4}$ ，则 $x - y =$ ；

(3)、拓展应用：若 $(2019 - m)^{2} + (m - 2020)^{2} = 7$ ，求 $(2019 - m)$ $(m - 2020)$ 的值.

查看试题解析
21. 端午节吃粽子是中华民族的传统习俗．某超市节前购进了甲、乙两种畅销口味的粽子．已知购进甲种粽子的金额是1200元，购进乙种粽子的金额是800元，购进甲种粽子的数量比乙种粽子的数量少50个，甲种粽子的单价是乙种粽子单价的2倍．

(1)、求甲、乙两种粽子的单价分别是多少元？

(2)、为满足消费者需求，该超市准备再次购进甲、乙两种粽子共200个，若总金额不超过1150元，问最多购进多少个甲种粽子？

查看试题解析
22. 已知A（-10，0），以0A为边在第二象限作等边△AOB

(1)、求点B的横坐标：

(2)、如下图，点M、N分别为OA、OB边上的动点，以MN为边在x轴上方作等边△MNE，连结OE，当∠EMO=45°时，求∠MEO的度数．

查看试题解析
23. 阅读材料：运用公式法分解因式，除了常用的平方差公式和完全平方公式以外，还可以应用其他公式，如立方和与立方差公式，其公式如下：
立方和公式： $x^{3} + y^{3} = (x + y) (x^{2} - x y + y^{2})$ ；
立方差公式： $x^{3} - y^{3} = (x - y) (x^{2} + x y + y^{2})$ .
根据材料和已学知识解决下列问题

(1)、因式分解： $a^{3} - 8$ ；

(2)、先化简，再求值： $(\frac{3 x}{x^{2} - 2 x} - \frac{x^{2} + 2 x + 4}{x^{3} - 8}) \div \frac{2}{x^{2} - 4}$ ，其中 $x = 3$ .

查看试题解析