鲁教版（五四学制）2022-2023学年七年级数学下册8.1 定理与命题 同步测试
试卷更新日期：2023-01-10 类型：同步测试
一、单选题
-
1. 下列命题中是真命题的是（ ）A、实数由有理数和无理数组成 B、实数分为正实数和负实数 C、若 ， 则a=b D、是个分数2. 下列说法错误的是（ ）A、过马路的斑马线是平行线 B、100米跑道的跑道线是平行线 C、若a∥b，b∥d，则a⊥d D、过直线外一点有且只有一条直线与已知直线平行3. 对于下列的叙述，其中错误的是（ ）A、两直线平行，同旁内角互补 B、同位角相等，两直线平行 C、过一点有且只有一条直线与已知直线平行 D、两点之间的所有连线中，线段最短4. 下列语句中，不是命题的是（ ）A、两点确定一条直线 B、同位角相等 C、垂线段最短 D、连接、两点5. 下列命题，是真命题的是（ ）A、两条直线被第三条直线所截，内错角相等 B、邻补角的角平分线互相垂直 C、相等的角是对顶角 D、若 ， ， 则6. 下面的语句是假命题的是（ ）A、同旁内角互补 B、钝角的补角是锐角 C、垂线段最短 D、直角的补角是直角7. a、b、c是同一平面内的三条直线，下列说法错误的是（ ）A、若a⊥b，b//c，则a⊥c B、若a⊥b，b⊥c，则a⊥c C、若a//b，b⊥c，则a⊥c D、若a//b，b//c，则a//c8. 有下列命题：①两条直线被第三条直线所截，同位角相等；②0.1的算术平方根是0.01；③算术平方根等于它本身的数是1；④如果点到两坐标轴的距离相等，则；⑤若 ， 则；⑥若 ， 则其中假命题的个数是（ ）A、1个 B、3个 C、5个 D、6个9. 下列命题中，是真命题的是（ ）A、同位角相等 B、有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、两条平行线间的距离处处相等10. 下列命题是真命题的是（ ）A、一个角的补角一定大于这个角 B、平行于同一条直线的两条直线平行 C、两条直线被第三条直线所截，同位角相等 D、相等的角是对顶角
二、填空题
-
11. 把“对顶角相等”改写成“如果…那么…”的形式 ．12. 已知命题“同旁内角互补”，这个命题是命题．（填“真”或“假”）13. 下列命题是真命题的有（填写相应序号）．
①对顶角相等；②两个锐角的和是钝角；③两直线平行，同旁内角互补；④一个正数与一个负数的和是负数．
14. 下列三个命题：①两个角的和等于平角时，这两个角互为邻补角；②两直线平行，内错角相等；③同旁内角互补，它们是真命题的是 ． （填序号）15. “同旁内角互补”，该命题是命题（选填“真”或“假”）．三、解答题
-
16. 判断下面命题的真假，若是假命题，请举出反例说明:
①一个三角形的3个内角中至少有1个钝角；
②若三条线段a ， b ， c满足a+b>c ， 则这三条线段a ， b ， c能够组成三角形；
③个位数字是5的整数，能被5整除；
④对于所有的自然数n ， 代数式n2-n+11的值都是质数；
17. 我们知道任何一个命题都由条件和结论两部分组成，如果我们把一个真命题的条件变结论，结论变条件，那么所得的命题是不是一个真命题？试举例说明．
18. 已知命题：“如图，点B、F、C、E在同一条直线上，则AB∥DE．”判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，在不添加其他辅助线的情况下，请添加一个适当的条件使它成为真命题，并加以证明．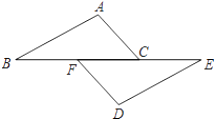
四、综合题
-
19. 如图，现有以下三个条件：①②③.请你以其中两个作为题设，另一个作为结论构造命题.
(1)、你构造的是哪几个命题？(2)、你构造的命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出反例（证明其中的一个命题即可）.20. 对于命题“相等的角是直角”，解决下列问题．(1)、指出命题的条件和结论，并改写成“如果…那么…”的形式；(2)、判断此命题是真命题还是假命题．21. 如图，有如下四个论断：① ， ② ， ③平分 ， ④平分 ．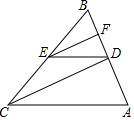
(1)、若选择四个论断中的三个作为条件，余下的一个论断作为结论，构成一个数学命题，其中正确的有哪些？不需说明理由．(2)、请你在上述正确的数学命题中选择一个进行说明理由．
