（人教版）2022-2023学年八年级数学下册17.2 勾股定理的逆定理同步测试

试卷更新日期：2023-01-10 类型：同步测试

进入出卷网下载

一、单选题

1. 下列各组数据中，不能作为直角三角形三边长的是（）

A、1，2，3 B、3，4，5 C、9，12，15 D、5，12，13

查看试题解析
2. 下列各组数是勾股数的是（）

A、5，12，14 B、6，8，12 C、4，5，6 D、7，24，25

查看试题解析
3. 两只蚂蚁在水平地面上从同一地点出发，一只以每分钟12cm的速度朝正东方向爬行，一只以每分钟16cm的速度朝正南方向爬行，10分钟之后两只蚂蚁相距（）

A、120cm B、160cm C、200cm D、280cm

查看试题解析
4. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B与灯塔P之间的距离为（）

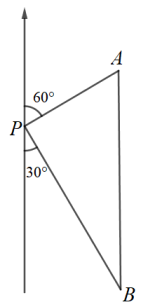A、60海里 B、45海里 C、20 $\sqrt{3}$ 海里 D、30 $\sqrt{3}$ 海里

查看试题解析
5. 满足下列条件的三边长为a、b、c的 $△ A B C$ ，不是直角三角形的是（）

A、 $b^{2} = a^{2} - c^{2}$ B、 $a ： b ： c = 3 ： 4 ： 5$ C、 $∠ C = ∠ B - ∠ A$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
6. 为加强疫情防控，云南某中学在校门口区域进行人校体温检测．如图，人校学生要求沿着直线AB单向单排通过校门口，测温仪C与直线AB的距离为3m，已知测温仪的有效测温距离为5m，则学生沿直线AB行走时测温的区域长度为（）

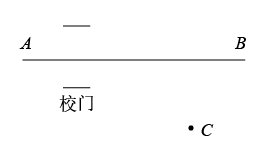A、4m B、5m C、6m D、8m

查看试题解析
7. 《九章算术》“勾股”章有一题：“今有二人同所立，甲行率七，乙行率三，乙东行，甲南行十步而斜东北与乙会，问甲、乙行各几何.”大意是说：已知甲、乙两人同时从同一地点出发，甲的速度为7，乙的速度为3，乙一直向东走，甲先向南走10步，后又向东北方向走了一段后与乙相遇，那么相遇时所用时间为多少？若设甲与乙相遇时间为x，则可列方程为（）

A、 $(3 x)^{2} + (7 x)^{2} = 1 0^{2}$ B、 $1 0^{2} + (7 x - 10)^{2} = (3 x - 10)^{2}$ C、 $(3 x)^{2} + 1 0^{2} = (7 x - 10)^{2}$ D、 $(3 x - 10)^{2} + (7 x)^{2} = 1 0^{2}$

查看试题解析
8. 在 $△ A B C$ 中，若 $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a，b，c，则下列条件中，不能判定 $△ A B C$ 是直角三角形的是（）

A、 $∠ A + ∠ B = 90 °$ B、 $a^{2} + b^{2} = c^{2}$ C、 $a = 3 k ， b = 4 k ， c = 5 k$ （k为正整数） D、 $a = 1 ， b = 2 ， c = 3$

查看试题解析
9. 如图，一个圆桶底面直径为8cm，高为12cm，则桶内所能容下的最长木棒的长度为（）．

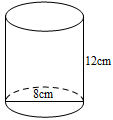A、8cm B、10cm C、 $4 \sqrt{5} c m$ D、 $4 \sqrt{13} c m$

查看试题解析
10. 如图，在△ABC中，∠B=90°，AB=1，BC=2．四边形ADEC是正方形，则正方形ADEC的面积是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 若直角三角形的两边长分别为3，4，则该直角三角形的斜边长为．

查看试题解析
12. 如图，甲、乙两艘客轮同时离开港口，航行的速度都是40m/min，甲客轮用15min到达点A，乙客轮用20min到达点B．若A，B两点的直线距离为1000m，甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向是．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 12 ， B C = 5$ ，分别 $A B 、 A C 、 B C$ 为边在 $A B$ 的同侧作正方形 $A B D E 、 A C F G 、 B C I H$ ，则图中阴影部分的周长为．

查看试题解析
14. 一根直立于水中的芦节（BD）高出水面（AC）2米，一阵风吹来，芦苇的顶端D恰好到达水面的C处，且C到BD的距离AC＝6米，水的深度（AB）为米

查看试题解析
15. 程大位所著《算法统宗》是一部中国传统数学重要的著作．在《算法统宗》中记载：“平地秋千未起，踏板离地一尺．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索长有几？”（1步=5尺）．译文：“当秋千静止时，秋干上的踏板离地有1尺高，如将秋千的踏板往前推动两步（10尺）时，踏板就和人一样高，美丽的姑娘和才子们，每天都来争荡秋千，欢声笑语终日不断．好奇的能工巧匠，能算出这秋千的绳索长是多少吗？”如图，假设秋千的绳索长始终保持直线状态，OA是秋千的静止状态，A是踏板，CD是地面，点B是推动两步后踏板的位置，弧AB是踏板移动的轨迹．已知 $A C = 1$ 尺， $C D = E B = 10$ 尺，人的身高 $B D = 5$ 尺，则 $O A =$ 尺．

查看试题解析

三、解答题

16. 如图，在一次地震中，一棵垂直于地面且高度为16米的大树被折断，树的顶部落在离树根8米处，即 $B C = 8$ ，求这棵树在离地面多高处被折断（即求AC的长度）？

查看试题解析
17. 八（2）班数学兴趣小组来到操场上测量旗杆 $A B$ 的高度，小强测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米（如图①），小云拉着绳子的下端往后退，当她将绳子拉直时，小晨测得此时小云拉绳子的手到地面的距离 $C D$ 为1米，到旗杆的距离 $C E$ 为8米（如图②），请你求出旗杆 $A B$ 的高度．

查看试题解析
18. 如图，一只小鸟旋停在空中A点，A点到地面的高度 $A B = 20$ 米，A点到地面C点（B、C两点处于同一水平面）的距离 $A C = 25$ 米．若小鸟竖直下降12米到达D点（D点在线段AB上），求此时小鸟到地面C点的距离．

查看试题解析

四、综合题

19. 如图，连接四边形ABCD的对角线AC，已知∠B=90°，BC=3，AB=4，CD=5，AD= $5 \sqrt{2}$ ．
求证：

(1)、AC=CD；

(2)、△ACD是直角三角形．

查看试题解析
20. 如图， $△ A B C$ 中， $A B = A C$ ， $B C$ 长为5，点D是 $A C$ 上的一点， $B D = 4 ， C D = 3$ ．

(1)、 $△ B C D$ 是哪种类型的三角形，请给出证明；

(2)、求出线段 $A C$ 的长．

查看试题解析
21. 已知a、b、c是 $△ A B C$ 的三边，且满足 $a^{4} + b^{2} c^{2} = b^{4} + a^{2} c^{2}$ ，试判断 $△ A B C$ 的形状.阅读下面解题过程：
解：由 $a^{4} + b^{2} c^{2} = b^{4} + a^{2} c^{2}$ 得：

$a^{4} - b^{4} = a^{2} c^{2} - b^{2} c^{2}$       ①

$(a^{2} + b^{2}) (a^{2} - b^{2}) = c^{2} (a^{2} - b^{2})$    ②

即 $a^{2} + b^{2} = c^{2}$       ③

∴ $△ A B C$ 为 $Rt △$ .      ④

(1)、试问：以上解题过程是否正确：

(2)、若不正确，请指出错在哪一步？（填代号）

(3)、本题的结论应为.

查看试题解析
22. 如图，在 $△ A B C$ 中，点D在AB上，连接CD， $A D = 4$ ， $C D = 2$ ， $B D = 1$ ， $B C = \sqrt{5}$ ．

(1)、求证： $C D ⊥ A B$ ；

(2)、求AC的长．

查看试题解析
23. 如图所示，在 $△ A B C$ 中，点D为BC边上的一点， $A D = 24$ ， $B D = 32$ ， $A B = 40$ ， $C D = 18$ ．

(1)、试说明 $A D ⊥ B C$ ；

(2)、求AC的长及 $△ A B C$ 的面积；

(3)、判断 $△ A B C$ 是否是直角三角形，并说明理由．

查看试题解析

（人教版）2022-2023学年八年级数学下册17.2 勾股定理的逆定理 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年八年级数学下册17.2 勾股定理的逆定理同步测试