（人教版）2022-2023学年八年级数学下册17.1 勾股定理同步测试

试卷更新日期：2023-01-10 类型：同步测试

进入出卷网下载

一、单选题

1. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时（即水平距离 $C D = 6 m$ ），踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是（） $m$

A、 $\frac{21}{2}$ B、 $\frac{15}{2}$ C、6 D、 $\frac{9}{2}$

查看试题解析
2. 如图，是我国汉代数学家赵爽为了证明勾股定理构造的图形，后人称之为“赵爽弦图”.该图形由四个全等的直角三角形拼接而成，若 $A F = 5$ ， $A B = 13$ ，则四边形 $E F G H$ 的面积为（）

A、25 B、49 C、64 D、144

查看试题解析
3. 如图，△ABD和△CBD，∠ADB=90°，∠ABD=∠DBC，AD=DC=1，若AB=4，则BC的长为（）

A、 $\frac{5}{2}$ B、2 $\sqrt{2}$ C、3 D、 $\frac{7}{2}$

查看试题解析
4. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ，以顶点 $A$ 为圆心， $A C$ 长为半径画弧，交 $A B$ 边于点 $D$ ，再分别以点 $C$ ， $D$ 为圆心，适当的长度为半径画弧，两弧交于点 $E$ ，作射线 $A E$ 交 $B C$ 边于点 $F$ ，点 $P$ 为边 $A B$ 上的动点，若 $B C = 3$ ，则 $P F$ 的取值范围是（）

A、 $\frac{1}{2} \leq P F \leq \frac{3}{2}$ B、 $1 \leq P F \leq 2$ C、 $\frac{3}{2} \leq P F \leq \frac{5}{2}$ D、 $2 \leq P F \leq 3$

查看试题解析
5. 如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S₁ ，小正方形面积为S₂ ，则（a+b）²可表示为（）

A、S₁-S₂ B、2S₁-S₂ C、S₁+S₂ D、S₁+2S₂

查看试题解析
6. 如图是两个全等的直角三角形拼成的图形，且点 $B$ ， $C$ ， $D$ 在同一直线上，连结 $A E .$ 设 $A B = a$ ， $B C = b$ ，则 $△ A C E$ 的面积可以表示为（）

A、 $a^{2} - b^{2}$ B、 $\frac{a^{2} - b^{2}}{2}$ C、 $a^{2} + b^{2}$ D、 $\frac{a^{2} + b^{2}}{2}$

查看试题解析
7. 如图，在等边△ABC中，AD平分∠BAC交BC于点D，点E为AC边的中点，BC=8；在AD上有一动点Q，则QC+QE的最小值为（　　）

A、4 $\sqrt{3}$ B、2 $\sqrt{3}$ C、4 D、8

查看试题解析
8. 数形结合是数学的重要思想和解题方法，如：“当0＜x＜12时，求代数式 $\sqrt{x^{2} + 4} + \sqrt{(12 - x)^{2} + 9}$ 的最小值”，其中 $\sqrt{x^{2} + 4}$ 可看作两直角边分别为x和2的Rt△ACP的斜边长， $\sqrt{(12 - x)^{2} + 9}$ 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值，如图所示，当AP与BP共线时，AP+BP为最小.请你解决问题：当0＜x＜4时，则代数式 $\sqrt{x^{2} + 1} + \sqrt{(4 - x)^{2} + 4}$ 的最小值是（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图， $△ A B C$ 是直角三角形，点C在数轴上对应的数为 $- 2$ ，目 $A C = 3$ ， $A B = 1$ ，若以点C为圆心， $C B$ 为半径画弧交数轴于点M，则A，M两点间的距离为（）

A、0.4 B、 $\sqrt{10} - 2$ C、 $\sqrt{10} - 3$ D、 $\sqrt{5} - 1$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，分别以AC，BC，AB为边在三角形外部作正方形．若以AC和BC为边的正方形面积分别为5和3，则以AB为边的正方形面积S的值为（）

A、4 B、8 C、 $2 \sqrt{2}$ D、34

查看试题解析

二、填空题

11. 如图，点B在射线AN上，以 $A B$ 为边作等边 $△ A B C$ ， M为 $A N$ 中点，且 $A N = 4$ ， P为 $B C$ 中点，当 $P M + P N$ 最小时， $A B =$ ．

查看试题解析
12. 如图，在△ABC中，∠ACB=90°，∠B=30°，AB=10，点D为斜边AB的中点，点P是直角边BC上一动点，连结AP，DP，则AP+DP的最小值为。

查看试题解析
13. 如图所示，在建筑工地上，为了支撑一堵墙，用一根长为5m的木材，顶端撑在墙上，底端撑在地面上， $B O = 4 m$ ，现为了增加支撑效果，底端向前移动 $1.5$ m，问：顶端需上移多少米？在这个问题中，设顶端上移x米，则可列方程为.

查看试题解析
14. 在△ABC中，AB＝AC＝5，BC＝6.若点P在边AC上移动，则BP的最小值是 .

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ，点 $P$ 为 $A C$ 边上的动点，过点 $P$ 作 $P D ⊥ A B$ 于点 $D$ ，则 $P B + P D$ 的最小值为.

查看试题解析

三、解答题

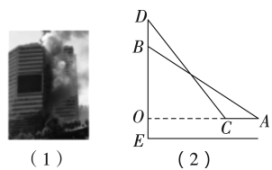
16. 某地一楼房发生火灾，消防队员决定用消防车上的云梯救人如图（1）.如图（2），已知云梯最多只能伸长到 $15 m$ （即 $A B = C D = 15 m$ ），消防车高 $3 m$ ，救人时云梯伸长至最长，在完成从 $12 m$ （即 $B E = 12 m$ ）高的 $B$ 处救人后，还要从 $15 m$ （即 $D E = 15 m$ ）高的 $D$ 处救人，这时消防车从 $A$ 处向着火的楼房靠近的距离 $A C$ 为多少米？（延长 $A C$ 交 $D E$ 于点 $O$ ， $A O ⊥ D E$ ，点 $B$ 在 $D E$ 上， $O E$ 的长即为消防车的高 $3 m$ ）

查看试题解析
17. 如图，小旭放风筝时，风筝挂在了树上，他先拉住风筝线，垂直于地面，发现风筝线多出1米；把风筝线沿直线BC向后拉5米，风筝线末端刚好接触地面，求风筝距离地面的高度AB.

查看试题解析
18. 如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，连结AE，求BE的长.

查看试题解析

四、综合题

19. 如图，在Rt△ABC中， $∠ A C B = 90 ° ， A B = 10 c m$ ， $A C ： B C = 3 ： 4$ ，动点P从B出发沿射线 $B C$ 以1 cm/s的速度运动，设运动时间为t（s）.

(1)、求 $B C$ 边的长.

(2)、当 $△ A B P$ 为等腰三角形时，求t的值.

查看试题解析
20. 在四边形 $A B C D$ 中， $Δ O A B$ 和 $Δ O C D$ 有公共顶点O，且 $Δ O A B ≌ Δ O C D$ .

(1)、如图1，O是边 $B C$ 上的一点.若 $A D ∥ B C$ .求证： $A O = D O$ .

(2)、如图1，O是边 $B C$ 上的一点.若 $∠ A O D = 80 °$ ，连接 $A C ， B D$ ，交点为E，求 $∠ D E C$ 的度数.

(3)、如图2，B、O、C三点不在一条线上，且 $∠ A O B = 90 °$ ，满足 $A D^{2} + B C^{2} = 50 ， A O = 3$ ，求 $Δ O A B$ 的面积.

查看试题解析
21. 如图，一根直立的旗杆高8m，因刮大风旗杆从点C处折断，顶部B着地且离旗杆底部A的距离为4m．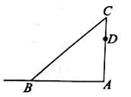

(1)、求旗杆距地面多高处折断（ $A C$ ）；

(2)、工人在修复的过程中，发现在折断点C的下方1m的点D处，有一条明显裂痕，将旗杆修复后，若下次大风将旗杆从点D处吹断，则距离旗杆底部周围多大范围内有被砸伤的风险？

查看试题解析
22. 等边 $△ ABC$ 中，点 $D$ ， $E$ 分别是边 $BC$ ， $AC$ 上的点，且 $CD = AE$ ， $AD$ ， $BE$ 交于点 $F$ .

(1)、求证： $△ ABE$ ≌ $△ CAD$ .

(2)、求 $∠ BFD$ 的度数.

(3)、若 $AF = 1$ ， $BF = 2$ ，则 $△ ABF$ 的面积为 $. ($ 直接写出答案 $)$

查看试题解析
23. 如图，点 $E$ ， $F$ 在 $C D$ 上，且 $∠ A E C = ∠ B F D = 90 °$ ， $A C = B D$ ， $C F = D E$ ．

(1)、求证： $Rt Δ AEC ≅ Rt Δ BFD$ ．

(2)、连结 $A F$ ，若 $A C = 5$ ， $A E = 3$ ， $C F = 1$ ，求 $A F$ 的长度．

查看试题解析

（人教版）2022-2023学年八年级数学下册17.1 勾股定理 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年八年级数学下册17.1 勾股定理同步测试