广东省佛山市顺德区2021-2022学年九年级下学期第一次教学质量数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. 如果 a与-2互为相反数,那么 a等于( )A、-2 B、2 C、 D、2. 的化简结果为( )A、3 B、-3 C、±3 D、93. 下面几何体的俯视图是圆的是( )A、
 B、
B、 C、
C、 D、
D、 4. 抛物线y=3(x﹣1)2+1的顶点坐标是( )A、(1,1) B、(﹣1,1) C、(﹣1,﹣1) D、(1,﹣1)5. 如图,直线 , 平分 , ,则 的度数是( )
4. 抛物线y=3(x﹣1)2+1的顶点坐标是( )A、(1,1) B、(﹣1,1) C、(﹣1,﹣1) D、(1,﹣1)5. 如图,直线 , 平分 , ,则 的度数是( )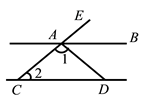 A、 B、 C、 D、6. 已知扇形的圆心角为 ,半径为 9,则弧长为( )A、 B、5π C、8π D、0π7. 2022 年北京冬奥会激起我校学生学习冬奥知识的热情.为了引领学生更深入地学习, 组织了一次知识竞赛,随机抽取 6 名同学的分数(单位:分)如下:80,90,85,92, 86,88,则这 6个数据的中位数是( )A、85 B、86 C、87 D、88.58. 如图,将正方形 ABCD 剪去 4个全等的直角三角形(图中阴影部分),得到边长为 c的四边形 EFGH.下列等式成立的是( )
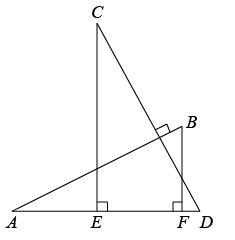
A、 B、 C、 D、6. 已知扇形的圆心角为 ,半径为 9,则弧长为( )A、 B、5π C、8π D、0π7. 2022 年北京冬奥会激起我校学生学习冬奥知识的热情.为了引领学生更深入地学习, 组织了一次知识竞赛,随机抽取 6 名同学的分数(单位:分)如下:80,90,85,92, 86,88,则这 6个数据的中位数是( )A、85 B、86 C、87 D、88.58. 如图,将正方形 ABCD 剪去 4个全等的直角三角形(图中阴影部分),得到边长为 c的四边形 EFGH.下列等式成立的是( ) A、a + b = c B、c2= (a + b )2 - 4ab C、c2= (a + b )(a - b ) D、a2+ b2= c29. 化简的结果是( )A、 B、 C、-3 D、10. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
A、a + b = c B、c2= (a + b )2 - 4ab C、c2= (a + b )(a - b ) D、a2+ b2= c29. 化简的结果是( )A、 B、 C、-3 D、10. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
 A、 B、 C、 D、11. 如图,数轴上的点 A、B 分别表示数 1、 . 则表示数的点P与线段 AB的位置关系是( )
A、 B、 C、 D、11. 如图,数轴上的点 A、B 分别表示数 1、 . 则表示数的点P与线段 AB的位置关系是( ) A、P 在线段AB上 B、P 在线段AB的延长线上 C、P 在线段AB的反向延长线上 D、不能确定12. 在△ABC中,∠BAC = 90°,AB=AC,D、E 是斜边 BC 上两点,且∠DAE=45°,将△ADC 绕点 A 顺时针旋转90° 得到△AFB, 连接 EF.下列结论:①BE⊥BF;②△ABC 的面积等于四边形 AFBD 的面积;③当 BE = CD 时,线段 DE 的长度最短.其中正确的个数( )
A、P 在线段AB上 B、P 在线段AB的延长线上 C、P 在线段AB的反向延长线上 D、不能确定12. 在△ABC中,∠BAC = 90°,AB=AC,D、E 是斜边 BC 上两点,且∠DAE=45°,将△ADC 绕点 A 顺时针旋转90° 得到△AFB, 连接 EF.下列结论:①BE⊥BF;②△ABC 的面积等于四边形 AFBD 的面积;③当 BE = CD 时,线段 DE 的长度最短.其中正确的个数( ) A、0 个 B、1 个 C、2 个 D、3 个
A、0 个 B、1 个 C、2 个 D、3 个二、填空题
-
13. 比较大小: sin 60°tan 30° (用“>”或“<”填空).14. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .15. 把多项式分解因式 .16. 如图, 为了测量操场上一棵大树的高度, 小明拿来一面镜子平放在离树根部 5m 的地面上,然后沿着树根和镜子所在的直线后退,当后退 1m 时,正好在镜中看见树的顶端.若小明的眼睛到地面的距离为1.5m ,则大树的高度是m.
 17. 有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形周长为 .
17. 有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形周长为 . 18. 二次函数y=ax2-2ax +c( a <0)的图象过 , , , 四个点.(1)、y3=(用关于 a或 c的代数式表示);(2)、若 <0时,则 0.(填“>”、“<”或“=”)
18. 二次函数y=ax2-2ax +c( a <0)的图象过 , , , 四个点.(1)、y3=(用关于 a或 c的代数式表示);(2)、若 <0时,则 0.(填“>”、“<”或“=”)三、解答题
-
19. 已知不等式组 ,(1)、解上述不等式组;(2)、从(1)的结果中选择一个整数是方程的解,求m的值.20. 如图,A,B,C,D 是⊙O 上的四个点,∠ADB =∠BDC = , 过点A作交CD延长线于点E.
 (1)、求∠ABC的大小;(2)、证明:AE 是⊙O 的切线.21. 为落实“垃圾分类回收,科学处理”的政策,某花园小区购买A、B两种型号的垃圾分类回收箱20只进行垃圾分类投放,共支付费用4320元.A、B型号价格信息如表:
(1)、求∠ABC的大小;(2)、证明:AE 是⊙O 的切线.21. 为落实“垃圾分类回收,科学处理”的政策,某花园小区购买A、B两种型号的垃圾分类回收箱20只进行垃圾分类投放,共支付费用4320元.A、B型号价格信息如表:型号
价格
A型
200元/只
B型
240元/只
(1)、请问小区购买A型和B型垃圾回收箱各多少只?(2)、因受到居民欢迎,准备再次购进A、B两种型号的垃圾分类回收箱共40只,其中A类的数量不大于 B 类的数量的2倍.求购买多少只A 类回收箱支出的费用最少,最少费用是多少元?22. 抛物线C1:y =-ax2-4(a -1)x -a+5(a ≠0).(1)、将C1先向右平移m个单位,再向下平移n个单位得到C2 , 点A(3,4-n)和点B(4, 6-2n)在上.当的对称轴为y轴时,求的表达式;(2)、求证:不论a为何值,抛物线与 x轴总有公共点.23. 已知∠MON=90°,点A , B分别在射线OM , ON上(不与点O重合),且OA>OB , OP平分∠MON , 线段AB的垂直平分线分别与OP , AB , OM交于点C , D , E , 连接CB , 在射线ON上取点F , 使得OF=OA , 连接CF . (1)、依题意补全图形;(2)、求证:CB=CF;(3)、用等式表示线段CF与AB之间的数量关系,并证明.24. 如图,点O是平面直角坐标系的原点,P是反比例函数(k > 0,x >0)图象上的动点,以P为圆心,PO为半径的圆与x、y轴分别交于点A,B,连接AB.
(1)、依题意补全图形;(2)、求证:CB=CF;(3)、用等式表示线段CF与AB之间的数量关系,并证明.24. 如图,点O是平面直角坐标系的原点,P是反比例函数(k > 0,x >0)图象上的动点,以P为圆心,PO为半径的圆与x、y轴分别交于点A,B,连接AB. (1)、求△OAB的面积;(2)、当 k =4时,求线段AB的最小值;(3)、在(2)的条件下,点C是反比例函数图象上的一点(不与点P重合),连接PC,AC.当∠ACP 是直角时,求点C横坐标的近似值(结果保留一位小数).
(1)、求△OAB的面积;(2)、当 k =4时,求线段AB的最小值;(3)、在(2)的条件下,点C是反比例函数图象上的一点(不与点P重合),连接PC,AC.当∠ACP 是直角时,求点C横坐标的近似值(结果保留一位小数).