安徽省淮北市五校2021-2022学年九年级下学期第一次月考数学试题

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

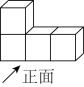
1. $- \frac{1}{2}$ 的相反数是（）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列运算结果中正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a^{3})}^{3} = a^{6}$ C、 ${(- 2 a)}^{3} = - 2 a^{3}$ D、 $a^{2} + a^{2} = 2 a^{2}$

查看试题解析
3. 2022年2月4日晚，北京冬奥会在国家体育场开幕，开幕式中使用的LED地面显示系统由4万块LED屏幕组成，全场的地面线缆总长超过20千米．数据“4万”可用科学记数法表示为（）．

A、 $0.4 \times 1 0^{5}$ B、 $4 \times 1 0^{4}$ C、 $4 \times 1 0^{5}$ D、 $4.0 \times 1 0^{3}$

查看试题解析
4. 如图是由四个相同的正方体组成的几何体，其俯视图是（）

A、 B、 C、 D、

查看试题解析
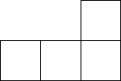5. 若关于x的一元二次方程 $x^{2} + x + m = 0$ 没有实数根，则m的取值范围是（）．

A、 $m > \frac{1}{4}$ B、 $m < \frac{1}{4}$ C、 $m < - \frac{1}{4}$ D、 $m \geq - \frac{1}{4}$

查看试题解析
6. 估计 $\sqrt{15} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 2021年安徽省固定资产投资比2020年增长9.4％，若2022年的增长率保持不变，2020年和2022年全省固定资产投资分别为a亿元和b亿元，则（）．

A、a（1＋9.4％）＝b B、a（1＋9.4％）（1＋7.3％）＝b C、a（1＋9.4％）²＝b D、a（1＋7.3％）²＝b

查看试题解析
8. 若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象如图所示，则二次函数 $y = x^{2} + k x - k$ 的图象可能是（）．

A、 B、 C、 D、

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $C D ⊥ A B$ ，点E为AC边上的中点，连接BE交CD于点F．若 $A C = 4 \sqrt{2}$ ，则BF的长为（）．

A、 $\frac{16}{3}$ B、4 C、 $\frac{2 \sqrt{10}}{3}$ D、 $\frac{4 \sqrt{10}}{3}$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 8$ ， $A C = 6$ ．若点P为直线BC上一点，且 $△ A B P$ 为等腰三角形，则符合条件的点P有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 分解因式： $4 - x^{4} =$ ．

查看试题解析
12. 为了解某校1000名九年级学生的视力情况，调查人员从中抽取了200名学生进行调查．在这个问题中，个体是．

查看试题解析
13. 如图，已知点B为 $\overset{⌢}{A C}$ 的中点，CD切 $⊙ O$ 于点C，点A，O，D在一条直线上．若 $∠ D = 36 °$ ，则 $∠ B A C =$ ．

查看试题解析
14. 如图，点M，N分别是矩形ABCD的边AD和对角线BD上的点，连接BM，MN， $A B = 1$ ， BC＝2

(1)、 $s i n ∠ A D B =$ ；

(2)、 $B M + M N$ 的最小值为．

查看试题解析

三、解答题

15. 解不等式组： ${\begin{array}{l} 2 (x - 1) - 1 > - 5 \\ - x + 2 > 3 x + 4 \end{array}$ ．

查看试题解析
16. 如图，在网格中，每个小正方形的边长为1个单位长度，AB是以格点（网格线的交点）为端点的线段，O是网格中一格点．
⑴将线段AB绕格点O顺时针旋转90°，得到线段CD（点A，B的对应点分别为点C，D），画出线段CD；
⑵以格点O为位似中心，在格点O的另一侧将 $△ O A B$ 放大为原来的2倍（即相似比为2∶1），得到 $△ O A_{1} B_{1}$ ，画出 $△ O A_{1} B_{1}$ ，并直接写出 $△ O A_{1} B_{1}$ 的面积．

查看试题解析
17. 观察下列各等式．
第1个等式： $4^{2} - 2^{2} = 12$
第2个等式： $6^{2} - 4^{2} = 20$
第3个等式： $8^{2} - 6^{2} = 28$
根据以上规律，解决下列问题．

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式：（用含n的等式表示），并证明．

查看试题解析
18. 如图，小明站在A处，准备测量教学楼CD的高度．此时他看向教学楼CD顶部的点D，发现仰角为45°．他向前走30m到达 $A^{'}$ 处，测得点D的仰角为67.5°．若小明的身高AB为1.8m（眼睛与头顶的距离忽略不计），则教学楼CD的高度为多少？（计算结果精确到0.1m，参考数据： $s i n 67.5 ° \approx 0.924$ ， $c o s 67.5 ° \approx 0.383$ ， $t a n 67.5 ° \approx 2.414$ ， $\sqrt{2} \approx 1.414$ ）

查看试题解析
19. 如图，一次函数 $y = - x + 4$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 在第一象限的图象交于 $A (1 ， n)$ 和B两点，与x轴交于点C．

(1)、求反比例函数的解析式；

(2)、直接写出当 $x > 0$ 时，不等 $- x + 4 < \frac{k}{x}$ 的解集；

(3)、求 $△ O A B$ 的面积．

查看试题解析
20. 如图，四边形ABCD内接于 $⊙ O$ ， $∠ B O D = 120 °$ ，四边形OBCD为菱形，连接AC．

(1)、求证：AC平分 $∠ B A D$ ；

(2)、若 $∠ A B O = 15 °$ ， $O B = 1$ ，求AD的长．

查看试题解析
21. 为了增加学生的阅读量，达到让学生“在阅读中成长，在成长中阅读”的效果，某中学计划在各班设立图书角．为合理搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对全校学生进行抽样调查．学校团委在收集整理了学生喜爱的书籍类型（A．科普、B．文学、C．体育、D．其他）数据后，绘制出两幅不完整的统计图，如图所示．
请你根据以上信息，解答下列问题．

(1)、随机抽样调查的样本容量是，扇形统计图中“B”所对应的圆心角的度数为度；

(2)、补全条形统计图；

(3)、抽样中选择文学类书籍的学生有2名男生和2名女生，校团委计划从中随机抽取2名学生参加团委组织的征文大赛，求恰好抽出一男一女的概率．

查看试题解析
22. 设二次函数 $y_{1}$ ， $y_{2}$ 的图象的顶点坐标分别为 $(a ， b)$ ， $(c ， d)$ ，若 $a = 2 c$ ， $b = 2 d$ ，且两图象开口方向相同，则称 $y_{1}$ 是 $y_{2}$ 的“同倍项二次函数”．

(1)、写出二次函数 $y = x^{2} + x + 1$ 的一个“同倍顶二次函数”；

(2)、已知关于x的二次函数 $y_{1} = x^{2} + n x$ 和二次函数 $y_{2} = x^{2} + 3 n x + 1$ ，若 $y_{1} + y_{2}$ 是 $y_{1}$ 的“同倍顶二次函数”，求n的值．

查看试题解析
23. 数学模型学习与应用．【学习】如图1， $∠ B A D = 90 °$ ， $A B = A D$ ， $B C ⊥ A C$ 于点C， $D E ⊥ A C$ 于点E．由 $∠ 1 + ∠ 2 = ∠ 2 + ∠ D = 90 °$ ，得∠1=∠D；又 $∠ A C B = ∠ A E D = 90 °$ ，可以通过推理得到 $△ A B C$ ≌ $△ D A E$ ．我们把这个数学模型称为“一线三等角”模型；

(1)、【应用】如图2，点B，P，D都在直线l上，并且 $∠ A B P = ∠ A P C = ∠ P D C = α$ ．若 $B P = x$ ， $A B = 2$ ， $B D = 5$ ，用含x的式子表示CD的长；

(2)、【拓展】在 $△ A B C$ 中，点D，E分别是边BC，AC上的点，连接AD，DE， $∠ B = ∠ A D E = ∠ C$ ， $A B = 5$ ， $B C = 6$ ．若 $△ C D E$ 为直角三角形，求CD的长；

(3)、如图3，在平面直角坐标系xOy中，点A的坐标为 $(2 ， 4)$ ，点B为平面内任一点． $△ A O B$ 是以OA为斜边的等腰直角三角形，试直接写出点B的坐标．

查看试题解析