安徽省蚌埠市2021-2022学年九年级下学期第一次月考数学试题

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 如图是由7个相同的小正方体搭成的几何体，则该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 二次函数 $y = {(x - 2)}^{2}$ 向右平移1个单位后的表达式是（）

A、 $y = (x - 3)^{2}$ B、 $y = (x - 1)^{2}$ C、 $y = (x - 2)^{2} + 1$ D、 $y = (x - 2)^{2} - 1$

查看试题解析
3. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 40 °$ ， $A B = 5$ ，则 $B C$ 的长为（）

A、 $5 t a n 40 °$ B、 $5 c o s 40 °$ C、 $5 s i n 40 °$ D、 $\frac{5}{c o s 40 °}$

查看试题解析
4. 若反比例函数 $y = \frac{k}{x}$ 的图像过点 $(1 ， \sqrt{6})$ ，则不在这个反比例函数图象上的点是（）

A、 $(\sqrt{3} ， \sqrt{2})$ B、 $(- \sqrt{2} ， - \sqrt{3})$ C、 $(\sqrt{6} ， 1)$ D、 $(2 ， 3)$

查看试题解析
5. 如图已知扇形 $A O B$ 的半径为 $6 c m$ ，圆心角的度数为 $12 0^{∘}$ ，若将此扇形围成一个圆锥的侧面，则围成的圆锥的底面积为（）

A、 $4 π c m^{2}$ B、 $6 π c m^{2}$ C、 $9 π c m^{2}$ D、 $12 π c m^{2}$

查看试题解析
6. 下列判断正确的是（）

A、任意掷一枚质地均匀的硬币10次，一定有5次正面向上 B、天气预报说“明天的降水概率为40%”，表示明天有40%的时间都在降雨 C、“篮球队员在罚球线上投篮一次，投中”为随机事件 D、“a是实数，|a|≥0”是不可能事件

查看试题解析
7. 在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (- 2 ， 4)$ ， $B (- 4 ， 0)$ ， $O (0 ， 0)$ ．以原点O为位似中心，把这个三角形缩小为原来的 $\frac{1}{2}$ ，得到 $△ C D O$ ，则点A的对应点C的坐标是（）

A、 $(- 1 ， 2)$ B、 $(1 ， - 2)$ C、 $(1 ， 2)$ D、 $(- 1 ， 2)$ 或 $(1 ， - 2)$

查看试题解析
8. 如图，⊙O的直径BA的延长线与弦DC的延长线交于点E，且CE=OB，已知∠DOB=72°，则∠E等于（）

A、36° B、30° C、18° D、24°

查看试题解析
9. 筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1，筒车盛水桶的运行轨道是以轴心 $O$ 为圆心的圆，如图2，已知圆心 $O$ 在水面上方，且 $⊙ O$ 被水面截得的弦 $A B$ 长为6米， $⊙ O$ 半径长为4米．若点 $C$ 为运行轨道的最低点，则点 $C$ 到弦 $A B$ 所在直线的距离是（）

A、1米 B、 $(4 - \sqrt{7})$ 米 C、2米 D、 $(4 + \sqrt{7})$ 米

查看试题解析
10. 如图，在矩形ABCD中，AB＝5，BC＝6，点E在BC边上，且BE＝2，F为AB边上的一个动点，连接EF，以EF为边作等边△EFG，且点G在矩形ABCD内，连接CG，则CG的最小值为（）

A、3 B、2.5 C、4 D、2 $\sqrt{3}$

查看试题解析

二、填空题

11. 已知点P是线段AB的黄金分割点，AP＞PB．若AB＝10．则AP＝（结果保留根号）．

查看试题解析
12. 如图， $⊙ O$ 是 $△ A B C$ 的内切圆，点D，E是切点， $∠ A = 50 °$ ， $∠ C = 60 °$ ，则 $∠ D O E =$ ．

查看试题解析
13. 如图，点A在双曲线y= $\frac{6}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ 上，AB $∥$ x轴，过点A作AD⊥x轴于D，连接OB，与AD相交于点C，若AB=2OD，则k的值为．

查看试题解析
14. 对于一个函数，自变量x取a时，函数值y也等于a，则称a是这个函数的不动点．已知二次函数 $y = x^{2} + 3 x + m$ ，

(1)、若2是此函数的不动点，则m的值为．

(2)、若此函数有两个相异的不动点a，b，且 $a < 1 < b$ ，则m的取值范围为．

查看试题解析

三、解答题

15. 求值： $\sin^{2} 45 ° + 3 \tan 30 ° \tan 60 ° - 2 \cos 60 °$

查看试题解析
16.

(1)、求x的值： 5：(x+1)=3：x .

(2)、已知线段a=2，b=8，求a，b的比例中项线段c.

查看试题解析
17. △ABC在平面直角坐标系中的位置如图，其中每个小正方形的边长为1个单位长度．
⑴画出△ABC关于原点O的中心对称图形△A₁B₁C₁；
⑵画出将△ABC绕点C顺时针旋转90°得到△A₂B₂C₂ ．
⑶在(2)的条件下，求点A旋转到点A₂所经过的路线长(结果保留π)．

查看试题解析
18. 如图，在航线 $l$ 的两侧分别有两个灯塔 $A$ 和 $B$ ，灯塔 $A$ 到航线 $l$ 的距离为 $A C = 3$ 千米，灯塔 $B$ 到航线 $l$ 的距离为 $B D = 4$ 千米，灯塔 $B$ 位于灯塔 $A$ 南偏东 $60 °$ 方向．现有一艘轮船从位于灯塔 $B$ 北偏西 $53 °$ 方向的 $N$ （在航线 $l$ 上）处，正沿该航线自东向西航行，10分钟后该轮船行至灯塔 $A$ 正南方向的点 $C$ （在航线 $l$ 上）处．

(1)、求两个灯塔 $A$ 和 $B$ 之间的距离；

(2)、求该轮船航行的速度（结果精确到0.1千米/小时）．（参考数据： $\sqrt{3} \approx 1.73$ ， $s i n 53 ° \approx 0.80$ ， $c o s 53 ° \approx 0.60$ ， $t a n 53 ° \approx 1.33$ ）

查看试题解析
19. 如图，已知一次函数 $y_{1} = k x + b$ 与反比例函数 $y_{2} = \frac{m}{x}$ 的图象在第一、三象限分别交于 $A (6 ， 1)$ ， $B (a ， - 3)$ 两点，连接 $O A$ ， $O B$ ．

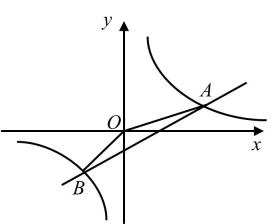(1)、求一次函数和反比例函数的解析式；

(2)、 $△ A O B$ 的面积为；

(3)、直接写出 $y_{1} > y_{2}$ 时x的取值范围．

查看试题解析
20. 如图，△ABC中，∠ABC＝90°，以AB为直径的⊙O交AB于点D，点E为BC的中点，连接OD、DE．

(1)、求证：OD⊥DE．

(2)、若∠BAC＝30°，AB＝8，求阴影部分的面积．

查看试题解析
21. 某单位食堂为全体名职工提供了 $A ， B ， C ， D$ 四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取240名职工进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查，根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：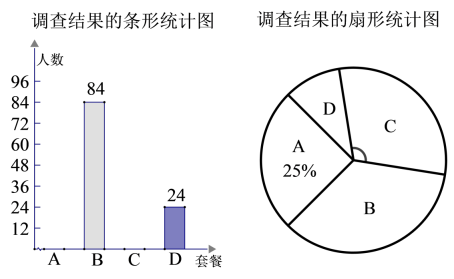

(1)、在抽取的 $240$ 人中最喜欢 $A$ 套餐的人数为，扇形统计图中“ $C$ ”对应扇形的圆心角的大小为；

(2)、依据本次调查的结果，估计全体 $960$ 名职工中最喜欢 $B$ 套餐的人数；

(3)、现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”，求甲被选到的概率．

查看试题解析
22. 如图， $A B$ 为半圆O的直径， $C B$ 为切线， $A C$ 交半圆O于点D，点E为 $\overset{⌢}{B D}$ 上一点，且 $\overset{⌢}{A D} = \overset{⌢}{D E}$ ， $B E$ 的延长线交 $A C$ 于点F，连接 $A E$ ．

(1)、求证∶ $∠ E A F = ∠ C$ ；

(2)、若 $B E = 1$ ， $E F = 2$ ，求 $B C$ 的长．

查看试题解析
23. 如图，在平面直角坐标系中，二次函数 $y = x^{2} + b x + c$ 的图像与x轴交于点． $A (- 1 ， 0)$ 、 $B (3 ， 0)$ ，与y轴交于点C．

(1)、 $b =$ ， $c =$ ；

(2)、若点D在该二次函数的图象上，且 $S_{△ A B D} = 2 S_{△ A B C}$ ，求点D的坐标；

(3)、若点P是该二次函数图象上位于x轴上方的一点，且 $S_{△ A P C} = S_{△ A P B}$ ，直接写出点P的坐标．

查看试题解析