上海市普陀区2021-2022学年九年级下学期4月月考数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. 的平方根是( )
A、±3 B、3 C、±9 D、92. 下列运算正确的是( )A、 B、 C、 D、3. 如果单项式2anb2c是六次单项式,那么n的值取( )A、6 B、5 C、4 D、34. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )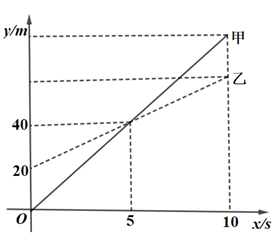 A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m5. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )
A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m5. 如图,正六边形ABCDEF内接于⊙O,半径为4,则这个正六边形的边心距OM和 的长分别为( )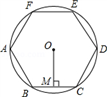 A、2, B、2 ,π C、 , D、2 ,6. 下列判断错误的是( )A、对角线互相垂直且相等的平行四边形是正方形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相平分的四边形是平行四边形
A、2, B、2 ,π C、 , D、2 ,6. 下列判断错误的是( )A、对角线互相垂直且相等的平行四边形是正方形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相平分的四边形是平行四边形二、填空题
-
7. 分解因式: =8. 不等式组的解集是 .9. 在正比例函数 中,y的值随着x值的增大而增大,则点 在第象限.10. 试写出一个二元二次方程,使该方程有一个解是 , 你写的这个方程是 (写出一个符合条件的即可).11. 方程的解是 .12. 关于x的一元二次方程有实数根,则a的取值范围是 .13. 对某次会议所用矿泉水的浪费情况进行调查,会议中每人发一瓶500毫升的矿泉水,会后对所发矿泉水喝的情况进行统计,分为四种情况:A.全部喝完;B.喝剩约;C.喝剩约一半;D.开瓶但基本未喝.根据统计结果绘制如下的两个统计图(不完整),则情况“C”所在扇形的圆心角度数为
 14. 如图,在△ABC中,点D在边AC上,AD=2CD,如果= , = , 那么= .
14. 如图,在△ABC中,点D在边AC上,AD=2CD,如果= , = , 那么= . 15. 从位男同学和位女同学中任选人参加志愿者活动,所选人中恰好是一位男同学和一位女同学的概率是 .16. 如图,在已知的△ABC中,按以下步骤作图:
15. 从位男同学和位女同学中任选人参加志愿者活动,所选人中恰好是一位男同学和一位女同学的概率是 .16. 如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,
连接CD.若CD=AC,∠A=50°,则∠ACB .
17. 新定义:已知三条平行直线, 相邻两条平行线间的距离相等, 我们把三个顺点分别在这样的三条平行 线上的三角形称为格线三角形. 如图, 已知等腰 Rt 为 “格线三角形”, 且 , 那么直线 与直线 的夹角 的余切值为 .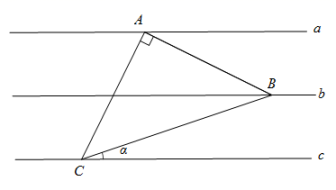 18. 如图, 已知在 Rt 中, , 将 绕点 逆时针旋转 后得 , 点 落在点 处, 点 落在点 处, 联结 , 作 的平分线 , 交线段 于点 , 交线 段 于点 , 那么 的值为 .
18. 如图, 已知在 Rt 中, , 将 绕点 逆时针旋转 后得 , 点 落在点 处, 点 落在点 处, 联结 , 作 的平分线 , 交线段 于点 , 交线 段 于点 , 那么 的值为 .
三、解答题
-
19. 计算:20. 先化简,再求值: , 其中;21. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
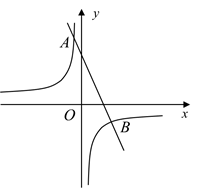 (1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.22. 如图,在某海滨城市附近海面有一股台风,据监测,当前台风中心位于该城市的南偏东方向200千米的海面处,并以20千米时的速度向处的北偏西的方向移动,台风侵袭范围是一个圆形区域,当前半径为60千米,且圆的半径以10千米时速度不断扩张.
(1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.22. 如图,在某海滨城市附近海面有一股台风,据监测,当前台风中心位于该城市的南偏东方向200千米的海面处,并以20千米时的速度向处的北偏西的方向移动,台风侵袭范围是一个圆形区域,当前半径为60千米,且圆的半径以10千米时速度不断扩张. (1)、当台风中心移动4小时时,受台风侵袭的圆形区域半径增大到千米:当台风中心移动小时时,受台风侵袭的圆形区域半径增大到千米;(2)、当台风中心移动到与城市距离最近时,这股台风是否侵袭这座海滨城市?请说明理由.参考数据 ,23. 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC.
(1)、当台风中心移动4小时时,受台风侵袭的圆形区域半径增大到千米:当台风中心移动小时时,受台风侵袭的圆形区域半径增大到千米;(2)、当台风中心移动到与城市距离最近时,这股台风是否侵袭这座海滨城市?请说明理由.参考数据 ,23. 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,点E在对角线BD上,作∠ECF=90°,连接DF,且满足CF=EC. (1)、求证:BD⊥DF;(2)、当时,试判断四边形DECF的形状,并说明理由.24. 如图,在平面直角坐标系中,抛物线与轴交于两点与轴交于点C,点M是抛物线的顶点,抛物线的对称轴与BC交于点D,与轴交于点E.
(1)、求证:BD⊥DF;(2)、当时,试判断四边形DECF的形状,并说明理由.24. 如图,在平面直角坐标系中,抛物线与轴交于两点与轴交于点C,点M是抛物线的顶点,抛物线的对称轴与BC交于点D,与轴交于点E. (1)、求抛物线的对称轴及B点的坐标(2)、如果 , 求抛物线的表达式;(3)、在(2)的条件下,已知点F是该抛物线对称轴上一点,且在线段的下方, , 求点的坐标25. 如图,线段 , 点是线段延长线上的点, , 点是线段延长线上的点, , 以为圆心,为半径作扇形 , . 点是弧上的点,联结、 .
(1)、求抛物线的对称轴及B点的坐标(2)、如果 , 求抛物线的表达式;(3)、在(2)的条件下,已知点F是该抛物线对称轴上一点,且在线段的下方, , 求点的坐标25. 如图,线段 , 点是线段延长线上的点, , 点是线段延长线上的点, , 以为圆心,为半径作扇形 , . 点是弧上的点,联结、 . (1)、联结交弧于 , 当时,求的长;(2)、当以为半径的和以为半径的相切时,求的值;(3)、当直线经过点 , 且满足时,求扇形的半径长.
(1)、联结交弧于 , 当时,求的长;(2)、当以为半径的和以为半径的相切时,求的值;(3)、当直线经过点 , 且满足时,求扇形的半径长.