上海市徐汇区2021-2022学年九年级下学期数学阶段性测试试题

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列代数式中，属于分式的是（）

A、 $\frac{x}{3}$ B、 $\frac{3}{x}$ C、 $\frac{\sqrt{x}}{\sqrt{3}}$ D、 $\frac{\sqrt{3}}{\sqrt{x}}$

查看试题解析
2. 下列结论中，不能由a+b=0得到的是（）

A、 $a^{2} = - a b$ B、 $a = 0 ， b = 0$ C、 $| a | = | b |$ D、 $a^{2} = b^{2}$

查看试题解析
3. 下列方程中，有实数根的是（）

A、 $x^{3} = - 1$ B、 $\sqrt{x^{4} + 1} = 0$ C、 $x^{2} + 5 x + 8 = 0$ D、 $\frac{x - 1}{x^{2}} = 1$

查看试题解析
4. 如果函数 $y = k x + 2$ 的图像不经过第三象限，那么k的取值范围是（）

A、 $k > 0$ B、 $k \geq 0$ C、 $k < 0$ D、 $k \leq 0$

查看试题解析
5. 如图，在四边形ABCD中，AC与BD相交于点O，∠BAD＝90°，BO＝DO，那么下列条件中不能判定四边形ABCD是矩形的是（）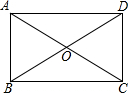

A、∠ABC＝90° B、∠BCD＝90° C、AB＝CD D、 $A B ∥ C D$

查看试题解析
6. 对于命题：①如果一个圆上所有的点都在另一个圆的内部，那么这个圆内含；②如果一个圆上所有的点都在另一个圆的外部，那么这个圆外离．下列判断正确的是（）

A、①是真命题，②是假命题 B、①是假命题，②是真命题 C、①、②都是真命题 D、①、②都是假命题

查看试题解析

二、填空题

7. 某机构对30万人的调查显示，沉迷于手机上网的初中生大约占7%，则这部分沉迷于手机上网的初中生人数，可用科学记数法表示为人．

查看试题解析
8. 方程 $\sqrt{x^{2} - 1} = x - 1$ 的解是．

查看试题解析
9. 函数 $y = \frac{\sqrt{x}}{x - 2}$ 中自变量 $x$ 的取值范围是．

查看试题解析
10. 如果关于x的方程 $3 x^{2} - k x + k = 0$ 有两个相等的实数根，那么k的值为．

查看试题解析
11. 已知反比例函数y＝ $\frac{k - 2}{x}$ ，当x＜0时，y随x的增大而减小，那么k的取值范围是．

查看试题解析
12. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相同，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各种多少两？设黄金重 $x$ 两，每枚白银重 $y$ 两，根据题意可列方程组为.

查看试题解析
13. 有四张质地相同的卡片，它们的背面相同，其中两张的正面印有“粽子”的图案，另外两张的正面印有“龙舟”的图案，现将它们背面朝上，洗均匀后排列在桌面，任意翻开两张，那么两张图案一样的概率是.

查看试题解析
14. 如果一个正六边形的边心距的长度为 $\sqrt{3} c m$ ，那么它的半径的长度为cm．

查看试题解析
15. 在植树节当天，某校一个班同学分成10个小组参加植树造林活动，10个小组植树的株数见下表：

植树株数（株）

5

6

7

小组个数

3

4

3

则这10个小组植树株数的方差是．

查看试题解析
16. 已知：P为△ABC的重心，连接BP并延长，交AC于点D．设 $\vec{A B} = \vec{a}$ 、 $\vec{B C} = \vec{b}$ ，则 $\vec{P D} =$ （请用含 $\vec{a}$ 、 $\vec{b}$ 的式子表示）；

查看试题解析
17. 人们把 $\frac{\sqrt{5} - 1}{2}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的 $0.618$ 法就应用了黄金分割数.设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，则 $a b = 1$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ ，…， $S_{10} = \frac{1}{1 + a^{10}} + \frac{1}{1 + b^{10}}$ .则 $S_{1} + S_{2} + \dots + S_{10} =$ .

查看试题解析
18. 如图，边长为2的正方形ABCD中，点E为AD的中点，连接BE，将△ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长．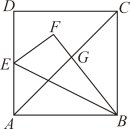

查看试题解析

三、解答题

19. 再求值： $\frac{x}{x + 4} - \frac{x^{2} + 4 x + 4}{x + 4} \div \frac{x^{2} - 4}{x - 2}$ ，其中x=2sin60°-（ $\frac{1}{2}$ ）^-2 ．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 15 - 9 x \leq 10 - 4 x ， \\ \frac{x - 1}{3} - \frac{x + 2}{6} > \frac{x}{2} - 2 \end{array}$ ，并将解集在数轴上表示出来．

查看试题解析
21. 在直角梯形ABCD中， $A B ∥ C D$ ， $∠ A B C = 90 °$ ， $∠ D A B = 60 °$ ， $A B = 2 C D$ ，对角线AC与BD相交于点O，线段OA，OB的中点分别为E，F．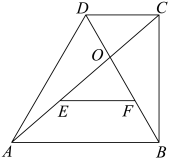

(1)、求证： $△ F O E ≌ △ D O C$ ；

(2)、求 $s i n ∠ O E F$ 的值．

查看试题解析
22. 如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．

查看试题解析
23. 如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB的中点，联结AE、EF，且AE⊥BE．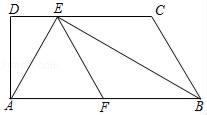

求证：

(1)、四边形BCEF是菱形；

(2)、BE•AE=2AD•BC．

查看试题解析
24. 如图所示，抛物线 $y = a (x + 1) (x - 5) (a \neq 0)$ 的图像与x轴交于A、B两点，与y轴交于点C．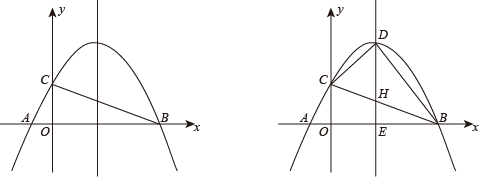

(1)、当 $a = - \frac{2}{5}$ 时，
①求点A、B、C的坐标；
②如果点P是抛物线上一点，点M是该抛物线对称轴上的点，当 $△ O M P$ 是以 $O M$ 为斜边的等腰直角三角形时，求出点P的坐标；

(2)、点D是抛物线的顶点，连接 $B D$ 、 $C D$ ，当四边形 $O B D C$ 是圆的内接四边形时，求a的值．

查看试题解析
25. 已知：在△ABC中， $∠ A B C = 90 °$ ， $A B = 5$ ， $∠ C = 30 °$ ，点D是AC边上一动点（不与A、C重合），过点D分别作 $D E ⊥ A B$ 交AB于点E， $D F ⊥ B C$ 交BC于点F，连接EF，设 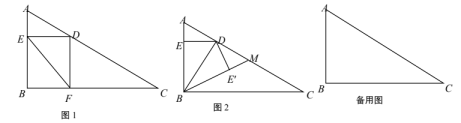$A E = x$ ， $E F = y$ ．

(1)、求y关于x的函数解析式，并写出定义域；

(2)、以F为圆心FC为半径的⊙F交直线AC于点G，当点G为AD中点时，求x的值；

(3)、如图2，联结BD将△EBD沿直线BD翻折，点E落在点 $E^{'}$ 处，直线 $B E^{'}$ 与直线AC相交于点M，当△BDM为等腰三角形时，求∠ABD的度数．

查看试题解析

植树株数（株）	5	6	7
小组个数	3	4	3