安徽省淮南市东部地区2021-2022学年九年级下学期第五次联考数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. 如图,在△ABC中,∠C=90°,AB=5 ,BC=3,则tanB的值是( )
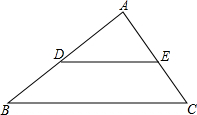
 A、 B、 C、 D、2. 下列各组的四条线段 , , , 是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,3. 如图,在△ABC中,点D、E分别在边AB,AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )
A、 B、 C、 D、2. 下列各组的四条线段 , , , 是成比例线段的是( )A、 , , , B、 , , , C、 , , , D、 , , ,3. 如图,在△ABC中,点D、E分别在边AB,AC上,连接CD、BE交于点O,且DE∥BC,OD=1,OC=3,AD=2,则AB的长为( )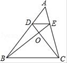 A、4 B、6 C、8 D、94. 在中, , 若的三边都缩小5倍,则的值( )A、放大5倍 B、缩小5倍 C、不变 D、无法确定5. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、6. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、7. 函数与在同一坐标系内的图象可以是( )A、
A、4 B、6 C、8 D、94. 在中, , 若的三边都缩小5倍,则的值( )A、放大5倍 B、缩小5倍 C、不变 D、无法确定5. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、6. 已知点 , , 都在反比例函数的图象上,则( )A、 B、 C、 D、7. 函数与在同一坐标系内的图象可以是( )A、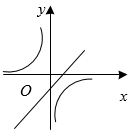 B、
B、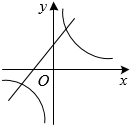 C、
C、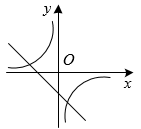 D、
D、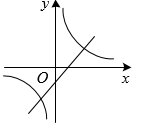 8. 如图,等边△ABC的边长为6,P为BC上一点,BP=2,D为AC上一点,若∠APD=60°,则CD的长为( )
8. 如图,等边△ABC的边长为6,P为BC上一点,BP=2,D为AC上一点,若∠APD=60°,则CD的长为( )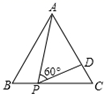 A、2 B、 C、 D、19. 如图,函数与函数的图象相交于A、B两点,轴,轴,则的面积等于( )
A、2 B、 C、 D、19. 如图,函数与函数的图象相交于A、B两点,轴,轴,则的面积等于( )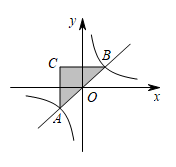 A、18 B、12 C、6 D、310. 如图,在边长为1的正方形网格中,连结格点 和 和 交于 , 为( )
A、18 B、12 C、6 D、310. 如图,在边长为1的正方形网格中,连结格点 和 和 交于 , 为( )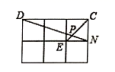 A、1 B、2 C、 D、
A、1 B、2 C、 D、二、填空题
-
11. 已知反比例函数y= ,当x>3时,y的取值范围是 .12. 比较大小:tan30° cos30°(用“>”或“<”填空)13. 在平面直角坐标系中,点A(﹣2,1),B(3,2),C(﹣6,m)分别在三个不同的象限.若反比例函数y= (k≠0)的图象经过其中两点,则m的值为.14. 如图,在直角坐标系中,第一象限内的点A,B都在反比例函数 的图象上,横坐标分别是3和1,点C在x轴的正半轴上,满足AC丄BC.且BC=2AC,则k的值是.

三、解答题
-
15. 计算:2cos30°-4sin45°+ .16. 如图,已知中, , 求BD的长.
 17. 在平面直角坐标系中,的三个顶点的坐标分别是 .
17. 在平面直角坐标系中,的三个顶点的坐标分别是 .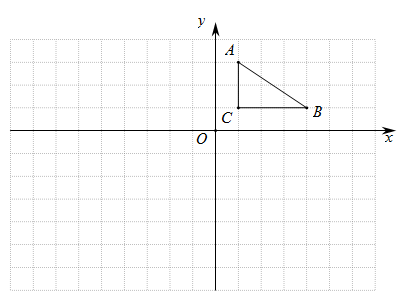
⑴画出关于x轴成轴对称的;
⑵画出以点O为位似中心,位似比为1∶2的 .
18. 为了有效保护环境,某景区要求游客将垃圾按可回收垃圾,不可回收垃圾,有害垃圾分类投放.一天,小林一家游玩了该景区后,把垃圾按要求分成三袋并随机投入三类垃圾桶中,请用列树状图的方法求三袋垃圾都投对的概率.19. 如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.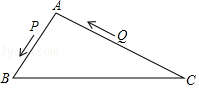 (1)、用含t的代数式表示:AP= , AQ=.(2)、当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?20. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)的山坡AB上发现棵古树CD,测得古树底端C到山脚点A的距离m,在距山脚点A处水平距离6m的点E处测得古树顶端D的仰角(古树CD与山坡AB的剖面、点E在同一平面上,古树CD所在直线与直线AE垂直),则古树CD的高度约为多少米?(结果精确到整数)(数据 , , )
(1)、用含t的代数式表示:AP= , AQ=.(2)、当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?20. 为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)的山坡AB上发现棵古树CD,测得古树底端C到山脚点A的距离m,在距山脚点A处水平距离6m的点E处测得古树顶端D的仰角(古树CD与山坡AB的剖面、点E在同一平面上,古树CD所在直线与直线AE垂直),则古树CD的高度约为多少米?(结果精确到整数)(数据 , , )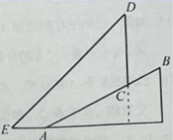 21. 如图,一次函数的图象与反比例函数的图象交于A,B两点,过点A做x轴的垂线,垂足为M,面积为1.
21. 如图,一次函数的图象与反比例函数的图象交于A,B两点,过点A做x轴的垂线,垂足为M,面积为1.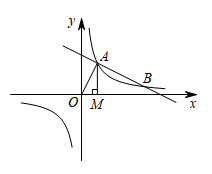 (1)、求反比例函数的解析式;(2)、在x轴上求一点P,使的值最大,并求出其最大值和P点坐标.22. 已知:如图,AB是 的直径,点E为 上一点,点D是 上一点,连接 并延长至点C,使 与AE交于点F.
(1)、求反比例函数的解析式;(2)、在x轴上求一点P,使的值最大,并求出其最大值和P点坐标.22. 已知:如图,AB是 的直径,点E为 上一点,点D是 上一点,连接 并延长至点C,使 与AE交于点F.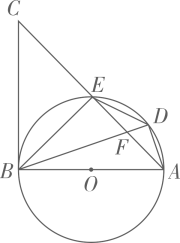 (1)、求证: 是 的切线;(2)、若 平分 ,求证: .23. 如图,在△ABC中,∠BCA=90°,BC=8,AC=6,点D是AB边上的中点,点E是BC边上的一个动点,连接DE,将△BDE沿DE翻折得到△FDE.
(1)、求证: 是 的切线;(2)、若 平分 ,求证: .23. 如图,在△ABC中,∠BCA=90°,BC=8,AC=6,点D是AB边上的中点,点E是BC边上的一个动点,连接DE,将△BDE沿DE翻折得到△FDE.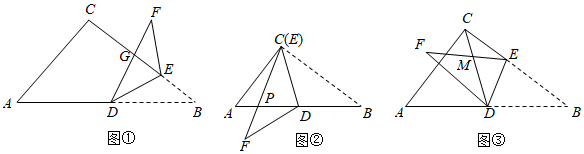 (1)、如图①,线段DF与线段BC相交于点G,当BE=2时,则;(2)、如图②,当点E与点C重合时,线段EF与线段AB相交于点P,求DP的长;(3)、如图③,连接CD,线段EF与线段CD相交于点M,当△DFM为直角三角形时,求BE的长.
(1)、如图①,线段DF与线段BC相交于点G,当BE=2时,则;(2)、如图②,当点E与点C重合时,线段EF与线段AB相交于点P,求DP的长;(3)、如图③,连接CD,线段EF与线段CD相交于点M,当△DFM为直角三角形时,求BE的长.