安徽省滁州市定远县吴圩片2021-2022学年九年级下学期5月调研考试数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. ﹣|﹣2022|的相反数为( )A、﹣2022 B、2022 C、﹣ D、2. 根据公布数据显示,2019年苏州市户籍人口约7 220 000人.数据“7 220 000”用科学记数法表示为 ( )A、 B、 C、 D、3. 如图是一个正方体沿四条棱的中点切割掉一部分后的示意图,该立体图的俯视图可能是( )
 A、
A、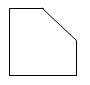 B、
B、 C、
C、 D、
D、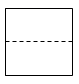 4. 下列说法:①把弯曲的河道改直,能够缩短航程,这是因为两点之间,线段最短:②若线段 , 则C是线段的中点;③一定是负数;④非负数的任何次幂都是非负数;⑤一个角的补角大于这个角本身.其中正确的个数为( )A、1 B、2 C、3 D、45. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D',C'的位置.若∠EFC'=115°,则∠AED'等于( )
4. 下列说法:①把弯曲的河道改直,能够缩短航程,这是因为两点之间,线段最短:②若线段 , 则C是线段的中点;③一定是负数;④非负数的任何次幂都是非负数;⑤一个角的补角大于这个角本身.其中正确的个数为( )A、1 B、2 C、3 D、45. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D',C'的位置.若∠EFC'=115°,则∠AED'等于( )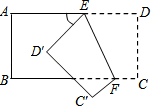 A、70° B、65° C、50° D、25°6. x,y分别是8-的整数部分和小数部分,则2xy-的值为( )A、3 B、4 C、5 D、67. 某农机厂四月份生产零件50万个,六月份生产零件182万个.设该厂平均每月的增长率为x,那么x满足的方程是( )A、 B、 C、 D、8. 如图所示,在△ABC中,AB=AC=5,BC=8,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
A、70° B、65° C、50° D、25°6. x,y分别是8-的整数部分和小数部分,则2xy-的值为( )A、3 B、4 C、5 D、67. 某农机厂四月份生产零件50万个,六月份生产零件182万个.设该厂平均每月的增长率为x,那么x满足的方程是( )A、 B、 C、 D、8. 如图所示,在△ABC中,AB=AC=5,BC=8,点E,F是中线AD上的两点,则图中阴影部分的面积是( ) A、6 B、12 C、24 D、309. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,方程a(x+1)(x-5)= -3的两根为x1和x2 , 且x1<x2 , 则下列结论正确的是( )
A、6 B、12 C、24 D、309. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,方程a(x+1)(x-5)= -3的两根为x1和x2 , 且x1<x2 , 则下列结论正确的是( )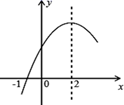 A、x1<-1<5<x2 B、x1<-1<x2<5 C、-1<x1<5<x2 D、-1<x1<x2<510. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于B、A两点,以线段AB为边在AB右侧作等边三角形ABC,边AC与x轴交于点E,边BC与y轴交于点F,点D是y轴上的一个动点,连接AD,BD,CD.下面的结论中,正确的是( )
A、x1<-1<5<x2 B、x1<-1<x2<5 C、-1<x1<5<x2 D、-1<x1<x2<510. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于B、A两点,以线段AB为边在AB右侧作等边三角形ABC,边AC与x轴交于点E,边BC与y轴交于点F,点D是y轴上的一个动点,连接AD,BD,CD.下面的结论中,正确的是( )①;②;③当时,;④点C的坐标为;⑤当时,;
 A、①③ B、②④⑤ C、①②③ D、①②③④⑤
A、①③ B、②④⑤ C、①②③ D、①②③④⑤二、填空题
-
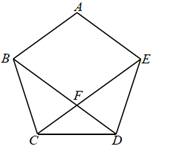
11. 要使式子有意义,则x的取值范围是 .12. 已知实数x、y、z满足x+y=5, ,那么 = .13. 如图,正五边形ABCDE的边长为2,对角线BD、CE相交于点F,则DF·BD的值为.
 14. 如图,抛物线与轴正半轴交于点 , 过点作轴交抛物线于点 , 抛物线的对称轴交抛物线于点、交轴于点 , 连结、、、 , 则四边形的面积为.
14. 如图,抛物线与轴正半轴交于点 , 过点作轴交抛物线于点 , 抛物线的对称轴交抛物线于点、交轴于点 , 连结、、、 , 则四边形的面积为.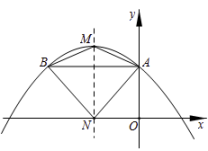
三、解答题
-
15.(1)、 .(2)、化简:先化简,再求值: , 其中x=3+ .16. 如图,在平面直角坐标系中,的三个顶点的坐标分别是 , , .
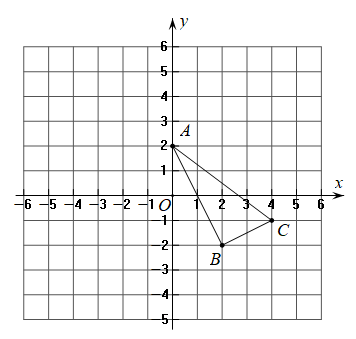
⑴在图中作出关于轴对称的;
⑵写出点的坐标为 ▲ ;
⑶在第一象限内作出一点 , 使 , , 连接 , .
17. 如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈ ,cos53°≈ ,tan53°≈ , ≈1.41) 18. 探究规律,完成下列题目.
18. 探究规律,完成下列题目.小明说:“我定义了一种新的运算,叫❈(加乘)运算.”然后他写出了一些按照❈(加乘)运算的法则进行运算的算式:(+5)❈(+2)=+7;(-3)❈(-5)=+8;(-3)❈(+4)=-7;(+5)❈(-6)=-11;0❈(+8)==8;(-6)❈0==6.
小颖看了这些算式后说:“我知道你定义的❈(加乘)运算的运算法则了.”聪明的你也看明白了吗?
(1)、归纳❈(加乘)运算的运算法则:①两数进行❈(加乘)运算时, .
②特别地,0和任何数进行❈(加乘)运算,或任何数和0进行❈(加乘)运算, .
(2)、计算:(-2)❈[0❈(-3)]= . (括号的作用同在有理数运算中的作用)(3)、我们知道加法有交换律和结合律,请你判断加法交换律在❈(加乘)运算中是否适用,并举例验证.(举一个例子即可)19. 如图,平面直角坐标系中,原点为 , 点、的坐标分别为、 , 的延长线交轴于点.点为线段上的一个动点,点从点沿方向以1个单位/秒的速度向运动,正方形边长为2(点在轴上,点、在轴右侧).设运动时间为秒.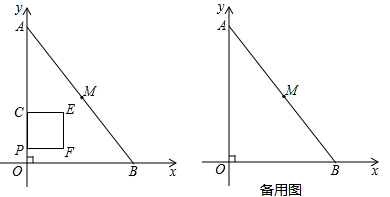 (1)、正方形的对角线所在直线的函数表达式为.(用含的式子表示),若正方形的对角线所在直线恰好经过点 , 则时间为秒.(2)、若正方形始终在内部运动,求的范围.(3)、在条件(2)下,设的面积为 , 求与的函数表达式.20. 某校八年级开展“学党史”知识竞赛活动.为了解本次竞赛成绩,张老师随机抽取了部分参赛同学的成绩(均为整数)进行统计,并绘制成成绩等级分布表、成绩扇形统计图、频数分布直方图(每组含左端点不含右端点,最后一组含100),具体如下:
(1)、正方形的对角线所在直线的函数表达式为.(用含的式子表示),若正方形的对角线所在直线恰好经过点 , 则时间为秒.(2)、若正方形始终在内部运动,求的范围.(3)、在条件(2)下,设的面积为 , 求与的函数表达式.20. 某校八年级开展“学党史”知识竞赛活动.为了解本次竞赛成绩,张老师随机抽取了部分参赛同学的成绩(均为整数)进行统计,并绘制成成绩等级分布表、成绩扇形统计图、频数分布直方图(每组含左端点不含右端点,最后一组含100),具体如下:成绩等级分布表
等级
成绩x/分
A
a≤x≤100
B
80≤x<a
C
60≤x<80
D
0≤x<60
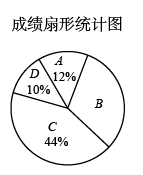
 (1)、共抽取了名同学的成绩,频数分布直方图中,m= , n=;(2)、已知在分数段90≤x≤100中的n名学生成绩的中位数为96分.强强同学的成绩为95分,则其成绩属于哪个等级?请说明理由;(3)、A等级和B等级中各有3人参加“学党史”交流会,A等级的3人为2名男生,1名女生,B等级的3人为1名男生,2名女生.若从A等级和B等级参加“学党史”交流会的学生中分别随机选出1人分享学习经验,求选中的2人恰好为一男一女的概率.21. 有一座抛物线形拱桥,桥下面在正常水位时 宽20 ,水位上升3 就达到警戒线 ,这时水面宽度为10 .
(1)、共抽取了名同学的成绩,频数分布直方图中,m= , n=;(2)、已知在分数段90≤x≤100中的n名学生成绩的中位数为96分.强强同学的成绩为95分,则其成绩属于哪个等级?请说明理由;(3)、A等级和B等级中各有3人参加“学党史”交流会,A等级的3人为2名男生,1名女生,B等级的3人为1名男生,2名女生.若从A等级和B等级参加“学党史”交流会的学生中分别随机选出1人分享学习经验,求选中的2人恰好为一男一女的概率.21. 有一座抛物线形拱桥,桥下面在正常水位时 宽20 ,水位上升3 就达到警戒线 ,这时水面宽度为10 . (1)、在如图的坐标系中,求抛物线的解析式.(2)、若洪水到来时,再持续多少小时才能到拱桥顶?(水位以每小时0.2 的速度上升)22. 如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E.
(1)、在如图的坐标系中,求抛物线的解析式.(2)、若洪水到来时,再持续多少小时才能到拱桥顶?(水位以每小时0.2 的速度上升)22. 如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E. (1)、求证:∠ABD=∠BCD;(2)、若DE=13,AE=17,求⊙O的半径;(3)、DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.23. 直线y=-x+5交x轴于点A,交y轴于点B,直线AC交y轴正半轴于点C, .(1)、求点C的坐标;(2)、如图1,过点B作BF⊥AB交x轴于点F,E为线段OF上一点,连接BE,设点E的横坐标为n,∠FBE的正切值为m,求m与n之间的函数关系式(不要求写出自变量n的取值范围);
(1)、求证:∠ABD=∠BCD;(2)、若DE=13,AE=17,求⊙O的半径;(3)、DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.23. 直线y=-x+5交x轴于点A,交y轴于点B,直线AC交y轴正半轴于点C, .(1)、求点C的坐标;(2)、如图1,过点B作BF⊥AB交x轴于点F,E为线段OF上一点,连接BE,设点E的横坐标为n,∠FBE的正切值为m,求m与n之间的函数关系式(不要求写出自变量n的取值范围); (3)、如图2,在(2)的条件下,D为线段AC上一点,作DG⊥BF于点G,连接DE、EG,当∠DEG=2∠FGE,m= 时,求sin∠FGE的值.
(3)、如图2,在(2)的条件下,D为线段AC上一点,作DG⊥BF于点G,连接DE、EG,当∠DEG=2∠FGE,m= 时,求sin∠FGE的值.