辽宁省抚顺市望花区2022年九年级下学期第四次质量检测数学试题

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列四个数中，最小的数是（）

A、 $- \frac{1}{3}$ B、 $- | - 3 |$ C、0 D、1

查看试题解析
2. 下列运算正确的是（）

A、 ${(a^{2})}^{3} = a^{6}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $a^{7} \div a = a^{7}$ D、 ${(- 2 a^{2})}^{3} = 8 a^{6}$

查看试题解析
3. 中学生骑电动车上学给交通安全带来隐患，为了解某中学2500个学生家长对“中学生骑电动车上学”的态度，从中随机调查了400个家长，结果有360个家长持反对态度，则下列说法正确的是（）

A、总体是中学生 B、样本容量是360 C、估计该校约有90%的家长持反对态度 D、该校只有360个家长持反对态度

查看试题解析
4. 以下是我国部分博物馆标志的图案，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 袁隆平院士被誉为“世界杂交水稻之父”，他研究的水稻，不仅高产，而且抗倒伏．在某次实验中，他的团队对甲、乙两种水稻品种进行产量稳定实验，各选取了8块条件相同的试验田，同时播种并核定亩产，结果甲、乙两种水稻的平均产量均为1200千克/亩，方差为 $S_{甲}^{2} = 186.9$ ， $S_{乙}^{2} = 325.3$ ．为保证产量稳定，适合推广的品种为（）

A、甲 B、乙 C、甲、乙均可 D、无法确定

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ，分别以点A、点B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，两弧相交于点M和点N，作直线MN分别交BC、AB于点D和点E，若 $∠ B = 50 °$ ，则 $∠ C A D$ 的度数是（）．

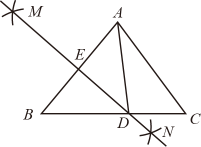A、20° B、30° C、40° D、50°

查看试题解析
7. 《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x人，物品价格为y钱，可列方程组为（）

A、 ${\begin{array}{l} y - 8 x = 3 \\ y - 7 x = 4 \end{array}$ B、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x - 4 = y \end{array}$ C、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 8 x - y = 3 \\ 7 x + y = 4 \end{array}$

查看试题解析
8. 如图，将线段 $A B$ 先绕原点 $O$ 按逆时针方向旋转 $90 °$ ，再向下平移4个单位，得到线段 $A' B'$ ，则点 $A$ 的对应点 $A'$ 的坐标是（）

A、 $(1 ， - 6)$ B、 $(- 1 ， 6)$ C、 $(1 ， - 2)$ D、 $(- 1 ， - 2)$

查看试题解析
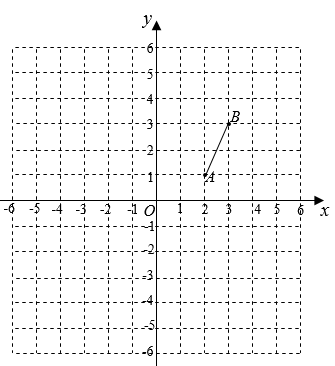9. 如图，在 $△ O A B$ 中， $∠ B O A = 45 °$ ，点C为边AB上一点，且 $B C = 2 A C$ ．如果函数 $y = \frac{9}{x} (x > 0)$ 的图象经过点B和点C，那么点C的坐标是（）

A、 $(3 ， 3)$ B、 $(3 ， 1.5)$ C、 $(4.5 ， 2)$ D、 $(9 ， 1)$

查看试题解析
10. 如图，已知抛物线 $y = a x^{2} + b x + c$ 的对称轴在y轴右侧，抛物线与x轴交于点 $A (- 2 ， 0)$ 和点B，与y轴的负半轴交于点C，且 $O B = 2 O C$ ，则下列结论：① $\frac{a - b}{c} > 0$ ；② $2 b - 4 a c = 1$ ；③ $a = \frac{1}{4}$ ；④ $c = 2 b - 1$ ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 中国人最早使用负数，可追溯到两千多年前的秦汉时期， $- 2$ 的相反数是．

查看试题解析
12. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
13. 冠状病毒是一大类病毒的总称．在电子显微镜下可以观察到它们的表面有类似日冕状突起，看起来像王冠一样，因此被命名为冠状病毒，其平均半径大约为0.00000005m；将0.00000005用科学记数法表示为．

查看试题解析
14. 在一个不透明的袋中装有若干个红球和4个黑球，每个球除颜色外完全相同．摇匀后从中摸出一个球，记下颜色后再放回袋中．不断重复这一过程，共摸球100次．其中有40次摸到黑球，估计袋中红球的个数是．

查看试题解析
15. 在一次体重测量中，九年级二班小明的体重为54.5kg，低于全班半数学生的体重，分析得到结论所用的统计量是．

查看试题解析
16. 王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC＝BC，∠ACB＝90°)，点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为cm.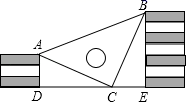

查看试题解析
17. 如图，数学知识在生产和生活中被广泛应用．下列实例所应用的最主要的几何知识为：
①射击时，瞄准星的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；
②车轮做成圆形，应用了“圆上各点到圆心的距离相等”；
③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；
④地板砖可以做成矩形，应用了“矩形对边相等”．
上述说法正确的是．（填序号）

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ， $A B = 2$ ．若点P是 $△ A B C$ 内一点，则 $P A + P B + P C$ 的最小值为．

查看试题解析

三、解答题

19. 先化简，再求值： $(\frac{a^{2}}{a - b} - \frac{2 a b - b^{2}}{a - b}) \div \frac{a - b}{a b}$ ，其中 $a = \sqrt{3} + 1 ， b = \sqrt{3} - 1$ ．

查看试题解析
20. 某中学为纪念“五一劳动节”，组织学生开展了书画展评活动，全校征集学生书画作品．王老师从全校18个班中随机抽取了A、B、C、D四个班，对征集作品进行了数量分析统计，绘制了如下两幅不完整的统计图．

(1)、王老师采取的调查方式是（填“全面调查”或“抽样调查”）；

(2)、王老师在所调查的4个班中，共征集到多少件作品？请求出并补全条形统计图；

(3)、如果全校参展作品中有4件获得一等奖，其中有1件作品的作者是男生，3件作品的作者是女生．现要从获得一等奖的学生中随机抽取两人去参加学校的总结表彰座谈会，请用树状图或列表的方法，求出恰好抽中一男一女的概率．

查看试题解析
21. 某商场计划购进一批甲、乙两种消毒液，已知甲种消毒液一瓶的进价与乙种消毒液一瓶的进价的和为40元，用90元购进甲种消毒液的瓶数与用150元购进乙种消毒液的瓶数相同．

(1)、求甲、乙两种消毒液每瓶的进价分别是多少元？

(2)、若购买甲、乙两种消毒液共50瓶，且总费用不超过1000元，求甲种消毒液至少要购买多少瓶？

查看试题解析
22. 在一次测量物体高度的数学实践活动中，小明从一条笔直公路上选择三盏高度相同的路灯进行测量．如图，他先在点B处安测倾器，于点A处测得路灯MN顶端的仰角为10°，再沿BN方向前进10m，到达点D处，于点C处测得路灯PQ顶端的仰角为45°．若测倾器AB的高度为1.5m，每相邻两根灯柱之间的距离相等，求路灯的高度（结果精确到0.1m）．
（参考数据： $s i n 10 ° \approx 0.17$ ， $c o s 10 ° \approx 0.98$ ， $t a n 10 ° \approx 0.18$ ）

查看试题解析
23. 如图，直线 $A B$ 经过 $⊙ O$ 上的点 $C$ ，直线 $B O$ 与 $⊙ O$ 交于点 $F$ 和点 $D$ ， $O A$ 与 $⊙ O$ 交于点 $E$ ，与 $D C$ 交于点 $G$ ， $O A = O B$ ， $C A = C B$ .

(1)、求证： $A B$ 是 $⊙ O$ 的切线；

(2)、若 $F C / / O A$ ， $C D = 6$ ，求图中阴影部分面积.

查看试题解析
24. 渠县是全国优质黄花主产地，某加工厂加工黄花的成本为30元/千克，根据市场调查发现，批发价定为48元/千克时，每天可销售500千克.为增大市场占有率，在保证盈利的情况下，工厂采取降价措施.批发价每千克降低1元，每天销量可增加50千克.

(1)、写出工厂每天的利润 $W$ 元与降价 $x$ 元之间的函数关系.当降价2元时，工厂每天的利润为多少元？

(2)、当降价多少元时，工厂每天的利润最大，最大为多少元？

(3)、若工厂每天的利润要达到9750元，并让利于民，则定价应为多少元？

查看试题解析
25. 在Rt $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ，点D为AB的中点，连接CD，将线段CD绕点D顺时针旋转 $α (60 ° < α < 120 °)$ 得到线段ED，且ED交线段BC于点G． $∠ C D E$ 的平分线DM交BC于点H．过点C作 $C F ∥ D E$ 交DM于点F，连接EF、BE．

(1)、如图1，若 $α = 90 °$ ，
①判断线段BE与DH的数量关系，并说明理由；
②求证： $\frac{B E}{F H} = \frac{\sqrt{3}}{3}$ ；

(2)、如图2，若 $A C = 2$ ， $t a n (α - 60 °) = m$ ，请直接写出 $\frac{B E}{F H}$ 的值（用含m的式子表示）．

查看试题解析
26. 如图1，已知抛物线 $y = a x^{2} + \frac{9}{4} x + c$ 与x轴交于A、B两点，与y轴交于C点，且点A的坐标为 $(- 1 ， 0)$ 、点C的坐标为 $(0 ， 3)$ ．

(1)、请写出该抛物线的函数表达式和点B的坐标；

(2)、如图2，有两动点D、E在 $△ C O B$ 的边上运动，运动速度均为每秒5个单位长度，它们分别从点C和点B同时出发，点D沿折线COB按C→O→B方向向终点B运动，点E沿线段BC按B→C方向向终点C运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t秒，请解答下列问题：
①当t为何值时， $△ B D E$ 的面积等于 $\frac{18}{5}$ ；
②在点D、E运动过程中，该抛物线上存在点F，使得依次连接AD、DF、FE、EA得到的四边形ADFE是平行四边形，请直接写出所有符合条件的点F的坐标．

查看试题解析