河北省石家庄长安区2022年九年级下学期3月份摸底数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. 下列条件中,不能确定一个圆的是( )A、圆心与半径 B、直径 C、平面上的三个已知点 D、三角形的三个顶点2. 如图,在△ABC中,D,E分别是AB,AC上的点, , 若AD=6,BD=3,AE=8,则EC的长是( )
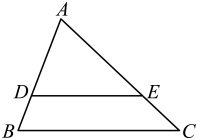 A、4 B、2 C、5 D、3. 用配方法解方程 , 下列配方正确的是( )A、 B、 C、 D、4. 抛物线的形状、开口方向与y=x2-4x+3相同,顶点在(-2,1),则关系式为( )A、y=(x-2)2+1 B、y=(x+2)2-1 C、y=(x+2)2+1 D、y=-(x+2)2+15. 如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
A、4 B、2 C、5 D、3. 用配方法解方程 , 下列配方正确的是( )A、 B、 C、 D、4. 抛物线的形状、开口方向与y=x2-4x+3相同,顶点在(-2,1),则关系式为( )A、y=(x-2)2+1 B、y=(x+2)2-1 C、y=(x+2)2+1 D、y=-(x+2)2+15. 如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )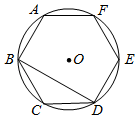 A、30° B、45° C、60° D、90°6. 两个反比例函数和 , 且 , 交点个数为( )A、0 B、2 C、4 D、无数个7. 小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A、30° B、45° C、60° D、90°6. 两个反比例函数和 , 且 , 交点个数为( )A、0 B、2 C、4 D、无数个7. 小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
A、 B、
B、 C、
C、 D、
D、 8. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)成绩如图所示,下列判断正确的是( )
8. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)成绩如图所示,下列判断正确的是( )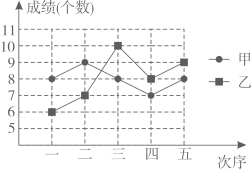 A、甲的成绩比乙稳定 B、甲的最好成绩比乙高 C、甲的成绩的平均数比乙大 D、甲的成绩的中位数比乙大9. 如果 , 且b是a,c的比例中项,那么等于( )A、4:3 B、3:2 C、2:3 D、3:410. 如图,在中,已知 , 以点C为圆心,为半径的圆交于点D,则的长为( )
A、甲的成绩比乙稳定 B、甲的最好成绩比乙高 C、甲的成绩的平均数比乙大 D、甲的成绩的中位数比乙大9. 如果 , 且b是a,c的比例中项,那么等于( )A、4:3 B、3:2 C、2:3 D、3:410. 如图,在中,已知 , 以点C为圆心,为半径的圆交于点D,则的长为( )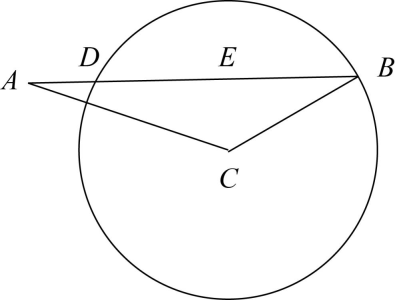 A、2 B、 C、或4 D、或11. 如图,以点为位似中心,把放大2倍得到 . 下列说法错误的是( )
A、2 B、 C、或4 D、或11. 如图,以点为位似中心,把放大2倍得到 . 下列说法错误的是( )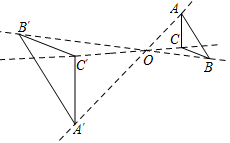 A、 B、 C、 D、直线经过点12. 下列说法中正确的是( )A、在Rt△ABC中,若tanA= , 则a=4,b=3 B、在Rt△ABC中,∠C=90°,若a=3,b=4,则tanA= C、tan30°+tan60°=1 D、tan75°=tan(45°+30°)=tan45°+tan30°=1+13. 已知一组数据的平均数为6,众数为5,则这组数据的中位数是( )A、4.5 B、5 C、5.5 D、614. 如图,已知点轴于点C.点P为线段上一点,且 . 则点P的坐标为( )
A、 B、 C、 D、直线经过点12. 下列说法中正确的是( )A、在Rt△ABC中,若tanA= , 则a=4,b=3 B、在Rt△ABC中,∠C=90°,若a=3,b=4,则tanA= C、tan30°+tan60°=1 D、tan75°=tan(45°+30°)=tan45°+tan30°=1+13. 已知一组数据的平均数为6,众数为5,则这组数据的中位数是( )A、4.5 B、5 C、5.5 D、614. 如图,已知点轴于点C.点P为线段上一点,且 . 则点P的坐标为( )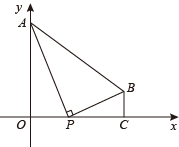 A、 B、 C、 D、15. 如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
A、 B、 C、 D、15. 如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )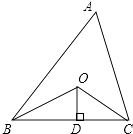 A、20 B、25 C、30 D、3516. 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )
A、20 B、25 C、30 D、3516. 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )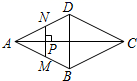 A、
A、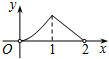 B、
B、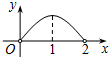 C、
C、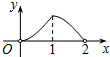 D、
D、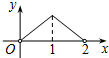
二、填空题
-
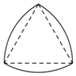
17. 一元二次方程x2﹣3x+1=0的根的判别式的值是 .18. 如图,分别以正三角形的3个顶点为圆心,边长为半径画弧,三段弧围成的图形称为莱洛三角形.若正三角形边长为6cm,则该莱洛三角形的周长为cm.
 19. 小刚要在边长为10的正方形内设计一个有共同中心O的正多边形,使其边长最大且能在正方形内自由旋转.如图1,若这个正多边形为正六边形;此时;若这个正多边形为正三角形,如图2,当正可以绕着点O在正方形内自由旋转时,的取值范围为 .
19. 小刚要在边长为10的正方形内设计一个有共同中心O的正多边形,使其边长最大且能在正方形内自由旋转.如图1,若这个正多边形为正六边形;此时;若这个正多边形为正三角形,如图2,当正可以绕着点O在正方形内自由旋转时,的取值范围为 .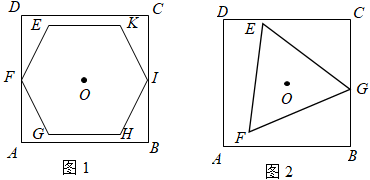
三、解答题
-
20. 已知中,都是锐角,且 ,(1)、分别求出三个内角度数;(2)、若 , 求长度.21. 【阅读材料】解方程(x-1)2-5(x-1)+4=0时,我们发现:先将x-1看作一个整体,然后设x-1=y.……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x-1=1,则x=2;当y=4时,x-1=4,则x=5,故原方程的解为x1=2,x2=5.
上述解题过程,在由原方程得到方程①的过程中,运用了“换元法”达到了解方程的目的,体现了转化的数学思想.
【解决问题】
(1)、请利用以上知识解方程:(3x+5)2-4(3x+5)+3=0;(2)、在△ABC中,∠C=90°,两条直角边的长分别为a,b,斜边的长为c,且(a2+b2)(a2+b2+1)=12,求斜边c的长.22. 如图,程序员在数轴上设计了A、B两个质点,它们分别位于-6和9的位置,现两点按照下述规则进行移动:每次移动的规则x分别掷两次正方体骰子,观察向上面的点数:
①若两次向上面的点数均为偶数,则A点向右移动1个单位,B点向左移2个单位;
②若两次向上面的点数均为奇数,则A点向左移动2个单位,B点向左移动5个单位;
③若两次向上面的点数为一奇一偶,则A点向右移动5个单位,B点向右移2个单位.
(1)、经过第一次移动,求B点移动到4的概率;(2)、从如图所示的位置开始,在完成的12次移动中,发现正方体骰子向上面的点数均为偶数或奇数,设正方体骰子向上面的点数均为偶数的次数为a,若A点最终的位置对应的数为b,请用含a的代数式表示b,并求当A点落在原点时,求此时B点表示的数;(3)、从如图所示的位置开始,经过x次移动后,若 , 求x的值.23. 如图,在平面直角坐标系中,反比例函数y=(x>0)的图像经过点A(1,2)和点B(m,n),且m>1,过点B作y轴的垂线,垂足为C.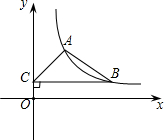 (1)、求该反比例函数的表达式;(2)、当时,求的面积;(3)、当的面积为2时,求点B的坐标.24. 在△ABC中,AD⊥BC,BC=AD=20cm,现有若干张长为5cm宽为3cm的矩形纸片,打算如图方向平铺在三角形内,(纸片均不能重叠和超出三角形ABC三边)
(1)、求该反比例函数的表达式;(2)、当时,求的面积;(3)、当的面积为2时,求点B的坐标.24. 在△ABC中,AD⊥BC,BC=AD=20cm,现有若干张长为5cm宽为3cm的矩形纸片,打算如图方向平铺在三角形内,(纸片均不能重叠和超出三角形ABC三边)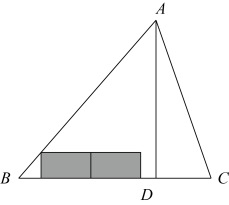 (1)、如果纸片只平铺底层,最多能平铺几张完整的矩形纸片,说明理由;(2)、三角形内最多可以平铺几张完整的矩形纸片,说明理由.25. 为了充分发挥科技导向作用,某公司计划建立总量为x(单位:万条)的行业数据库,经过调研发现;运行总成本y(单位1万元)由基础成本、技术成本、维护成本三部分组成,其中基础成本保持不变为500万元,技术成本与x成正比例,维护成本与x的平方成正比例,运行中得到如下数据,
(1)、如果纸片只平铺底层,最多能平铺几张完整的矩形纸片,说明理由;(2)、三角形内最多可以平铺几张完整的矩形纸片,说明理由.25. 为了充分发挥科技导向作用,某公司计划建立总量为x(单位:万条)的行业数据库,经过调研发现;运行总成本y(单位1万元)由基础成本、技术成本、维护成本三部分组成,其中基础成本保持不变为500万元,技术成本与x成正比例,维护成本与x的平方成正比例,运行中得到如下数据,x(单位:万条)
200
300
y(单位:万元)
700
860
(1)、求y与x之间的函数关系式,(2)、该公司为了实现数据共享,计划吸收会员,每名会员需交纳会员费30万元,已知会员数Q与x之间的关系式为 , 且时, , 且此时公司的利润W(单位:万元)最大,求m、n的值(利润=会员费-运行总成本).26. 在如图1所示的平面直角坐标系中,O为原点, ⊙C的圆心坐标为(−2,−2),半径为 , 直线y=−x+2与x轴,y轴分别交于点A,B,点P在线段AB上运动(包括端点).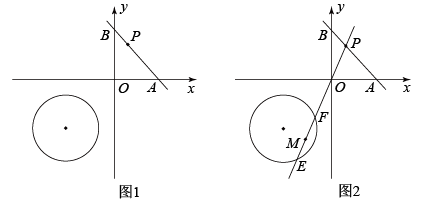 (1)、直线CO与AB的夹角是;(2)、当是等腰三角形时,求点P的坐标;(3)、当直线与相切时,求的度数;(4)、如图2.直线与相交于点E,F,M为线段的中点,当点P在线段上运动时,点M也相应运动,请直接写出点M所经过路径的长度.
(1)、直线CO与AB的夹角是;(2)、当是等腰三角形时,求点P的坐标;(3)、当直线与相切时,求的度数;(4)、如图2.直线与相交于点E,F,M为线段的中点,当点P在线段上运动时,点M也相应运动,请直接写出点M所经过路径的长度.