安徽省淮北市2022年“百校联赢”中考数学大联考试卷（3月份）

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 比-2小3的数是（）

A、-5 B、-1 C、1 D、5

查看试题解析
2. 根据地区生产总值统一核算结果，2021年安徽省生产总值42959.2亿元，比上年增长8.3%，两年平均增长6%．其中“42959.2亿”用科学记数法表示为（）

A、42959.2×10⁸ B、4.29592×10¹¹ C、4.29592×10¹² D、42.9592×10¹³

查看试题解析
3. a²•（-a）³的运算结果是（）

A、a⁵ B、-a⁵ C、a⁶ D、-a⁶

查看试题解析
4. 一个几何体的三视图如图所示，那么这个几何体是（）

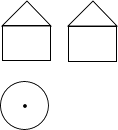A、 B、 C、 D、

查看试题解析
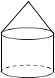5. 已知不等式组 ${\begin{array}{l} x + 2 < 3 \\ \frac{1 - x}{3} \leq 1 \end{array}$ ，其解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，有一个角为30°的直角三角板放置在一个长方形直尺上，若∠1=18°，则∠2的度数为（）

A、162° B、142° C、138° D、135°

查看试题解析
7. 一个蓄水池有水50m³ ，打开放水闸门匀速放水，水池中的水量和放水时间的关系如表，则放水14min后，水池中还有水（）
放水时间（min）
1
2
3
4
…
水池中水量（m³）
48
46
44
42
…

A、22m³ B、24m³ C、26m³ D、28m³

查看试题解析
8. 某直播带货公司去年12月份的营业额为a元，春节期间该公司营业额一直增长，若该公司今年元月和2月的营业额的月平均增长率为x，则该公司今年2月份营业额比去年12月营业额增长了（）

A、a（2+x）x元 B、a（1+x）²元 C、a（1+x）元 D、a（1+x）x元

查看试题解析
9. 如图所示，方格纸中是小天设计的跳棋线路图，每个小方格的边长为一个单位长度，有一枚棋子P从点A出发，每次向右或向下跳一个单位长度，且向右或向下跳是等可能的，那么棋子P经过3次跳动后恰好是沿着小天设计的路线到达点B的概率为（）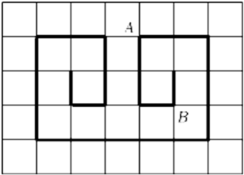

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{3}{8}$

查看试题解析
10. 等腰△ABC中，AB＝AC，以腰AB为直径的圆O，与底边BC交于P，若圆O与腰AC的交点Q关于直线AP的对称点落在线段OA上（不与端点重合），则下列说法正确的是（）

A、∠BAC＞60° B、30°＜∠ABC＜60° C、BP＞ $\frac{1}{2}$ AB D、 $\frac{1}{2}$ AC＜PQ＜ $\frac{\sqrt{2}}{2}$ AC

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{8}$ -（-1）⁰＝．

查看试题解析
12. 因式分解 $a x^{2} - 4 a$ = ．

查看试题解析
13. 如图，△ABC内接于⊙O，∠A＝30°，∠C＝45°，BD⊥AC于D，若⊙O的半径是5 $\sqrt{2}$ ，则BD的长为．

查看试题解析
14. 如图，在菱形ABCD中，∠ABC＝120°，AB＝10，点M、N分别在边AD、AB上．

(1)、对角线AC的长是；

(2)、若将△AMN沿MN翻折得到△PMN，点P恰好是边CD的中点，则AN的长是．

查看试题解析

三、解答题

15. 解分式方程： $\frac{1}{x - 1}$ +3＝ $\frac{2 - x}{1 - x}$ ．

查看试题解析
16. 如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均在格点（网格线的交点）上，线段PQ在网格线上．

(1)、画出△ABC关于线段PQ所在直线对称的△A₁B₁C₁；

(2)、将△A₁B₁C₁绕点B₁逆时针旋转90°得到△A₂B₁C₂ ，画出△A₂B₁C₂ ．

查看试题解析
17. 校园雕塑是校园文化的重要载体，在中国科学技术大学校园中有一座郭沫若的雕像，雕像由像体AD和底座CD两部分组成，小天同学在地面B处测出点A和点D的仰角分别是70.5°和45°，测得CD＝2.3米，求像体AD的高度．（结果精确到0.1米，参考数据：sin70.5°≈0.943，cos70.5°≈0.334，tan70.5°≈2.824）

查看试题解析
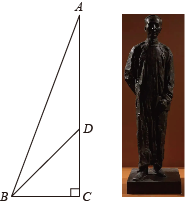18. 古希腊科学家把一定数目的点在等距离的排列下可以形成一个三角形，构成这些三角形点的数量被称为三角形数．某数学兴趣小组对三角形数进行了如下探索：

(1)、如图，将围棋子摆成连续三角形探索连续三角形数（ $a_{n}$ 表示第n个三角形数），由图形可得 $a_{1} = 1$ ， $a_{2} = 3$ ， $a_{3} = 6$ ， $a_{4} = 10$ ， $a_{5} =$ ；

(2)、为探索 $a_{n}$ 的值，将摆成三角形进行旋转 $180 °$ ，再与原图拼成一个矩形，通过矩形计算棋子数目达到计算 $2 a_{n}$ 的值，∴ $2 a_{n} =$ ；（用含n的代数式表示）

(3)、根据上面的结论，判断24和28是不是三角形数？并说明理由．

查看试题解析
19. 如图，反比例函数y＝ $\frac{m}{x}$ （m≠0）的图象与一次函数y＝kx+3（k≠0）的图象交于点A（-4，-1）和点B．

(1)、求点B的坐标；

(2)、求△AOB的面积．

查看试题解析
20. 如图，在⊙O 中，AB 是⊙O 的直径，AC＝AD，AB 交 CD 于 E，直径 CM 交 AD 于 N，连接 DM．

(1)、求证：AB $∥$ DM；

(2)、若 OE＝4，ON＝2，求⊙O 的半径．

查看试题解析
21. 为了解某校学生对“四史”的了解情况，校团委从本校学生随机抽取60名学生进行测试，获得了他们的成绩（百分制），按照40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100进行分组，绘制频数分布直方图如图．

(1)、求频数分布直方图中x的值；

(2)、判断这60名同学成绩的中位数在哪一组；

(3)、设各组平均分如表：
组别
40～50
50～60
60～70
70～80
80～90
90～100
平均分
45
55
65
75
85
95
根据以上信息，估计这次测试成绩的平均分（结果取整数）．

查看试题解析
22. 已知抛物线y＝ax²+bx-3（a，c是常数，a≠0）经过A（-1，-2），B（1，-6）．

(1)、求抛物线y＝ax²+bx-3的函数解析式；

(2)、抛物线有两点M（2，y₁）、N（m，y₂），当y₁＜y₂时，求m的取值范围．

查看试题解析
23. 如图 1，在正方形ABCD中，M、N分别为边AB、AD上的点，连接CM、CN，且CM＝CN．

(1)、求证：△BMC≌△DNC；

(2)、如图2，若P是边BC上的点，且NP⊥CM于O，连接OA，求证：OM+ON＝ $\sqrt{2}$ OA；

(3)、如图3，在满足（2）的条件下，过O作OQ⊥BC于Q，若AM＝2BM，求 $\frac{O Q}{C D}$ 的值．

查看试题解析

放水时间（min）	1	2	3	4	…
水池中水量（m³）	48	46	44	42	…

组别	40～50	50～60	60～70	70～80	80～90	90～100
平均分	45	55	65	75	85	95