湖南省长沙市雅礼集团2022-2023学年八年级上学期第三次月考数学试卷

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 2022年冬奥会将在北京举行，以下历届冬奥会会徽是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2020年1月24日，中国疾控中心成功分离我国首株新型冠状病毒毒种，该毒种直径约为0.00008毫米，则0.00008用科学记数法表示为（）

A、 $0.8 \times 1 0^{- 7}$ B、 $8 \times 1 0^{- 5}$ C、 $8 \times 1 0^{- 6}$ D、 $80 \times 1 0^{- 6}$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{5}$ B、 $2 a + 3 a = 6 a$ C、 $a^{8} \div a^{2} = a^{4}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
4. 如图，在 $△$ ABC中，AB＝AC，AD平分∠BAC，则下列结论错误的是（）

A、∠B＝∠C B、AD⊥BC C、∠BAD＝∠CAD＝∠C D、BD＝CD

查看试题解析
5. 不等式组 ${\begin{array}{l} x \geq - 2 \\ x \leq 1 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 《孙子算经》中有这样一个数学问题：今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，木长多少尺？小明同学准备用二元一次方程组解决这个问题，他已列出一个方程是 $x - y = 4.5$ ，则符合题意的另一个方程是（）

A、 $\frac{1}{2} x + 1 = y$ B、 $2 x + 1 = y$ C、 $\frac{1}{2} x - 1 = y$ D、 $2 x - 1 = y$

查看试题解析
7. 如图，点E，D分别在 $A B ， A C$ 上，若 $∠ B = 30 °$ ， $∠ C = 55 °$ ，则 $∠ 1 + ∠ 2$ 的度数为（）

A、 $85 °$ B、 $80 °$ C、 $75 °$ D、 $70 °$

查看试题解析
8. 下列各式由左到右的变形中，属于分解因式的是（）

A、 $a (m + n) = a m + a n$ B、 $a^{2} - b^{2} - c^{2} = (a + b) (a - b) - c^{2}$ C、 $x^{2} - 16 + 8 x = (x + 4) (x - 4) + 8 x$ D、 $10 x^{2} - 5 x = 5 x (2 x - 1)$

查看试题解析
9. 要调查下列问题，适合采用抽样调查的是（）

A、疫情期间，了解全校师生入校时体温情况 B、检测我国研制的C919大飞机的零件的质量 C、调查某批次汽车的抗撞击能力 D、选出某校短跑最快的学生参加全市比赛

查看试题解析
10. 如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ=PQ，PR=PS，则下列四个结论：①PA平分∠BAC；②AS=AR；③QP∥AR；④△BRP≌△CSP，其中结论正确的的序号为（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题

11. 分解因式： $a^{2} - a b$ = ．

查看试题解析
12. 若分式 $\frac{3}{x + 5}$ 有意义，则 $x$ 的取值范围是 .

查看试题解析
13. 已知 $a^{m} = 2$ ， $a^{n} = 3$ （ $m, n$ 为正整数），则 $a^{3 m + 2 n} =$ .

查看试题解析
14. 如图， $∠ A C D = 90 °$ ， $∠ D = 15 °$ ， $B$ 点在 $A D$ 的垂直平分线上，若 $A C = 4$ ，则 $A B$ 为.

查看试题解析
15. 如果x²-mx＋81是一个完全平方式，那么m的值为.

查看试题解析
16. 如图， $∠ A O B = 60 °$ ，点 $P$ 在 $∠ A O B$ 的角平分线上， $O P = 10 c m$ ，点 $E$ 、 $F$ 是 $∠ A O B$ 两边 $O A$ 、 $O B$ 上的动点，当 $△ P E F$ 的周长最小时，点 $P$ 到 $E F$ 距离是.

查看试题解析

三、解答题

17. 计算： $(π - \sqrt{2022})^{0} - {(\frac{1}{2})}^{- 2} + \sqrt[3]{- 8} - | 1 - \sqrt{2} |$ .

查看试题解析
18. 因式分解：

(1)、 $2 x^{2} - 2$ ；

(2)、 $3 x^{2} - 18 x + 27$ .

查看试题解析
19. 先化简再求值 $(\frac{x}{x + 2} + \frac{x^{2} + 2 x}{x^{2} - 4}) \div \frac{x}{x - 4}$ ，其中 $x = 1$ .

查看试题解析
20. 近年来，中学生的身体素质普遍下降，某校为了提高本校学生的身体素质，落实教育部门“在校学生每天体育锻炼时间不少于 $1$ 小时”的文件精神，对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图：
组别
$A$
$B$
$C$
$D$
时间 $t$ （分钟）
$t < 40$
$40 \leq t < 60$
$60 \leq t < 80$
$80 \leq t < 100$
人数
12
30
$a$
24

(1)、本次被调查的学生数为；

(2)、统计表中 $a =$ ，扇形统计图 $B$ 部分圆心角为度；

(3)、根据调查结果，请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.

查看试题解析
21. 如图，△ABC是等边三角形，BD是AC边上的高，延长BC至E，使DB=DE.

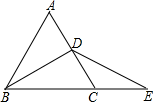(1)、求∠BDE的度数；

(2)、求证：△CED为等腰三角形.

查看试题解析
22. 某体育馆计划从一家体育用品商店一次性购买若干个气排球和篮球（每个气排球的价格都相同，每个篮球的价格都相同）.经洽谈，购买1个气排球和2个篮球共需210元；购买2个气排球和3个篮球共需340元.

(1)、每个气排球和每个篮球的价格各是多少元？

(2)、该体育馆决定从这家体育用品商店一次性购买气排球和篮球共50个，总费用不超过3200元，且购买气排球的个数少于30个，有哪几种购买方案？

查看试题解析
23. 如图，在△ $A B C$ 中，AD⊥BC，垂足为D，AD＝CD，点E在AD上，DE＝BD＝2，M、N分别是AB、CE的中点.

(1)、求证：△ADB≌△CDE；

(2)、求∠MDN的度数.

(3)、若CD＝5，求△AMD的面积.

查看试题解析
24. [项目学习]配方法是数学中重要的一种思想方法.它是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法，这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题.
例如，把二次三项式 $x^{2} - 2 x + 3$ 进行配方.
解： $x^{2} - 2 x + 3 = x^{2} - 2 x + 1 + 2 = (x^{2} - 2 x + 1) + 2 = {(x - 1)}^{2} + 2$ .
我们定义：一个整数能表示成 $a^{2} + b^{2}$ （ $a$ ， $b$ 是整数）的形式，即两个数的平方和形式，则称这个数为“雅美数”例如，5是“雅美数”.理由：因为 $5 = 2^{2} + 1^{2}$ .再如， $M = x^{2} + 2 x y + 2 y^{2} = {(x + y)}^{2} + y^{2}$ （ $x$ ， $y$ 是整数），所以 $M$ 也是“雅美数”.

(1)、[问题解决]4，6，7，8四个数中的“雅美数”是.

(2)、若二次三项式 $x^{2} - 6 x + 13$ （ $x$ 是整数）是“雅美数”，可配方成 ${(x - m)}^{2} + n$ （ $m$ ， $n$ 为常数），则 $m n$ 的值为；

(3)、[问题探究]已知 $S = x^{2} + 4 y^{2} + 8 x - 12 y + k$ （ $x$ ， $y$ 是整数， $k$ 是常数且 $x \neq - 4$ ， $y \neq \frac{3}{2}$ ），要使 $S$ 为“雅美数”，试求出符合条件的 $k$ 值.

(4)、[问题拓展]已知实数 $M$ ， $N$ 是“雅美数”，求证： $M \cdot N$ 是“雅美数”.

查看试题解析
25. 已知 $A (m ， 0)$ ， $B (0 ， n)$ ，满足： $| n - 4 | + \sqrt{m + n} = 0$ .

(1)、求 $m$ 和 $n$ 的值；

(2)、如图，点 $D$ 是A点左侧的 $x$ 轴上一动点，连接 $B D$ ，以 $B D$ 为直角边作等腰直角 $△ B D E$ ，连接 $A B$ 、 $E A$ ， $E A$ 交 $B D$ 于点 $G$ .
①求证： $∠ A E D = ∠ A B D$ ；
②当 $A B = A D$ 时，求证： $A E$ 平分 $∠ B E D$ .

查看试题解析

组别	$A$	$B$	$C$	$D$
时间 $t$ （分钟）	$t < 40$	$40 \leq t < 60$	$60 \leq t < 80$	$80 \leq t < 100$
人数	12	30	$a$	24