湖南省湘西土家族苗族自治州凤凰县2022-2023学年七年级上学期12月学情诊断数学试题

试卷更新日期：2023-01-10 类型：月考试卷

进入出卷网下载

一、单选题

1. $- \frac{1}{3}$ 的相反数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $\pm \frac{1}{3}$

查看试题解析
2. 单项式 $- 2 x y^{3}$ 的系数与次数分别是（）

A、-2，4 B、2，3 C、-2，3 D、2，4

查看试题解析
3. 下列方程为一元一次方程的是（　　）

A、y+3=0 B、x+2y=3 C、x²=2x D、 $\frac{1}{y}$ +y=2

查看试题解析
4. 若 $| b + 3 |$ 与 ${(a - 2)}^{2}$ 相为相反数，则 $a + b$ 的值为（）

A、-1 B、-5 C、5 D、1

查看试题解析
5. 下列去括号正确的是（）

A、+2（a-b）＝2a-b B、-2（a-b）＝-2a-2b C、-2（a-b）＝-2a+b D、-2（a-b）＝-2a+2b

查看试题解析
6. 如果 $\frac{1}{2} x^{m} y$ 和 $- x^{2} y^{n}$ 是同类项，则 $m + n =$ （）

A、3 B、2 C、1 D、-1

查看试题解析
7. 有理数a，b在数轴上对应点的位置如图所示，下列各式正确的是（）

A、 $a + b < 0$ B、 $a - b < 0$ C、 $a b > 0$ D、 $\frac{a}{b} > 0$

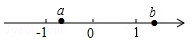查看试题解析
8. 日常生活中，我们用十进制来表示数，如3516＝3×10³+5×10²+1×10¹+6×1．计算机中采用的是二进制，即只需要0和1两个数字就可以表示数．如二进制中的1010＝1×2³+0×2²+1×2¹+0×1，可以表示十进制中的10．那么，二进制中的110101表示的是十进制中的（）

A、25 B、23 C、55 D、53

查看试题解析
9. 已知ab $>$ 0，则 $\frac{a}{| a |}$ + $\frac{| b |}{b}$ + $\frac{a b}{| a b |}$ 的值是（）

A、3 B、－3 C、3或－1 D、3或－3

查看试题解析
10. 已知整数 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …满足下列条件： $a_{1} = 0$ ， $a_{2} = - | a_{1} + 1 |$ ， $a_{3} = - | a_{2} + 2 |$ ， $a_{4} = - | a_{3} + 3 |$ ， ……依此类推，则 $a_{2022}$ 的值为（）

A、2022 B、-2022 C、-1011 D、1011

查看试题解析

二、填空题

11. 甲、乙两人同时从某地出发，如果甲向东走 $250 m$ 记作 $+ 250 m$ ，则乙走了 $- 150 m$ 表示.

查看试题解析
12. 2013年11月，习近平来到湘西十八洞村考察，首次对扶贫工作作出重要指示，强调“扶贫要实事求是，因地制宜.要精准扶贫，切忌喊口号，也不要定好高骛远的目标”.经过全国人民的共同努力，目前农村贫困人口减少11090000人，脱贫攻坚取得决定性成就.把数11090000用科学记数法表示为.

查看试题解析
13. 化简: $| π - 4 | + | 3 - π |$ =

查看试题解析
14. 一个多项式加上5x²﹣4x﹣3得﹣x²﹣3x，则这个多项式为．

查看试题解析
15. 根据“ $x$ 的2倍与3的和比 $x$ 的二分之一少4”可列方程：.

查看试题解析
16. 已知x=2是关于x的一元一次方程-2ax=x+a的解，则a的值为.

查看试题解析
17. 如图，若开始输入的x的值为正整数，最后输出的结果为144，则满足条件的x的值为．

查看试题解析
18. 某超市推出如下优惠方案：
①一次性购物不超过100元不享受优惠；
②一次性购物超过100元但不超过300元，一律9折
③一次性购物超过300元，一律8折
小李两次购物分别付款80元，252元，如果他一次性购买以上两次相同的商品，应付款

查看试题解析

三、解答题

19. 计算：

(1)、 $10 - (- 5) + 8 \div (- 4)$

(2)、 $6 \times \frac{1}{2} - (- 1)^{3} + (- 2)^{2} + | - 2 |$

查看试题解析
20. 解方程： $x - \frac{3 - x}{2} = \frac{x}{4} + 1$

查看试题解析
21. 将下列各数填在相应的集合里.
-3.8，-20%，4.3，-∣- $\frac{20}{7}$ ∣， $4^{2}$ ，0，-（- $\frac{3}{5}$ ）, $- 3^{2}$

整数集合：{              …}；

分数集合：{              …}；

正数集合：{              …}；

负数集合：{              …}.

查看试题解析
22. 先化简，再求值
多项式－2－（2a－3b+1）－(3a+2b)，其中a=－3，b=－2

查看试题解析
23. 原来从张家界到怀化坐普通列车需要3.5小时，当中国“最美扶贫高铁”之一的“张吉怀高铁”修通后，高铁运行里程比原来普通列车缩短了40千米，现在从张家界到怀化坐高铁只需要1小时.已知高铁的平均速度比普通列车的平均速度每小时快200千米，求高铁的平均速度.

查看试题解析
24. 已知数轴上三点M，O，N对应的数分别为﹣2，0，4，点P为数轴上任意一点，其对应的数为x.

(1)、如果点P到点M点N的距离相等，则x＝.

(2)、数轴上是否存在点P，使点P到点M、点N的距离之和是10？若存在，求出x的值；若不存在，请说明理由.

(3)、如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等，求t的值.

查看试题解析
25. 定义：若整数k的值使关于x的方程 $\frac{x + 4}{2} + 1 = k x$ 的解为整数，则称k为此方程的“友好系数”.

(1)、判断当 $k = 1$ 时是否为方程 $\frac{x + 4}{2} + 1 = k x$ 的“友好系数”，写出判断过程；

(2)、方程 $\frac{x + 4}{2} + 1 = k x$ “友好系数”的个数是有限个数，还是无穷多？如果是有限个数，求出此方程的所有“友好系数”；如果是无穷多，说明理由.

查看试题解析
26. 阅读理解：在解形如 $3 | x - 2 | = | x - 2 | + 4$ 这类含有绝对值的方程时，
解法一：我们可以运用整体思想来解.移项得 $3 | x - 2 | - | x - 2 | = 4$ ， $2 | x - 2 | = 4$ ，
$| x - 2 | = 2$ ， $x - 2 = \pm 2$ ， $x = 4$ 或 $x = 0$ .
解法二：运用分类讨论的思想，根据绝对值的意义分 $x < 2$ 和 $x \geq 2$ 两种情况讨论：
①当 $x < 2$ 时，原方程可化为 $- 3 (x - 2) = - (x - 2) + 4$ ，解得 $x = 0$ ，符合 $x < 2$ ；
②当 $x \geq 2$ 时，原方程可化为 $3 (x - 2) = (x - 2) + 4$ ，解得 $x = 4$ ，符合 $x \geq 2$ .
$∴$ 原方程的解为 $x = 0$ 或 $x = 4$ .
解题回顾：本解法中2为 $x - 2$ 的零点，它把数轴上的点所对应的数分成了 $x < 2$ 和 $x \geq 2$ 两部分，所以分 $x < 2$ 和 $x \geq 2$ 两种情况讨论.
问题：结合上面阅读材料，解下列方程：

(1)、解方程： $| x - 3 | + 8 = 3 | x - 3 |$

(2)、解方程： $| 2 - x | - 3 | x + 1 | = x - 9$

查看试题解析