广西南宁三十七中、三中联考2022-2023学年九年级上学期12月月考数学试题
试卷更新日期:2023-01-10 类型:月考试卷
一、单选题
-
1. 下列图案中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是随机事件的是( )A、太阳绕着地球转 B、在一个标准大气压下,水加热到100℃沸腾 C、负数大于正数 D、明天下大雨3. 如图,已知圆的内接正六边形的边长为6,则圆的半径为( )
2. 下列事件中,是随机事件的是( )A、太阳绕着地球转 B、在一个标准大气压下,水加热到100℃沸腾 C、负数大于正数 D、明天下大雨3. 如图,已知圆的内接正六边形的边长为6,则圆的半径为( ) A、6 B、4 C、3 D、24. 一元二次方程x2+2x+2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根5. 当压力时,物体所受的压强p(单位:)关于受力面积S(单位:)的函数图象大致是( )A、
A、6 B、4 C、3 D、24. 一元二次方程x2+2x+2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、无实数根5. 当压力时,物体所受的压强p(单位:)关于受力面积S(单位:)的函数图象大致是( )A、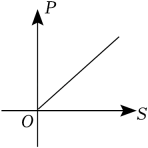 B、
B、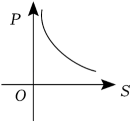 C、
C、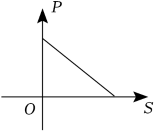 D、
D、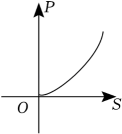 6. 将二次函数的图象向左平移5个单位长度,再向下平移6个单位长度,得到的函数图象的关系式是( )A、 B、 C、 D、7. 如图,绕点O逆时针旋转得到 , 若 , 则的度数是( )
6. 将二次函数的图象向左平移5个单位长度,再向下平移6个单位长度,得到的函数图象的关系式是( )A、 B、 C、 D、7. 如图,绕点O逆时针旋转得到 , 若 , 则的度数是( ) A、 B、 C、 D、8. 如图,圆锥的底面半径 , 高 , 则圆锥的侧面积是( )
A、 B、 C、 D、8. 如图,圆锥的底面半径 , 高 , 则圆锥的侧面积是( ) A、36π B、60π C、64π D、48π9. 如表是二次函数的自变量x与函数值y的部分对应值,那么方程的一个根的取值范围是( )
A、36π B、60π C、64π D、48π9. 如表是二次函数的自变量x与函数值y的部分对应值,那么方程的一个根的取值范围是( )x
…
1
1.1
1.2
1.3
1.4
…
y
…
-1
-0.49
0.04
0.59
1.16
…
A、 B、 C、 D、10. 如图,分别与⊙O相切于E、F、G三点,且 , cm,cm,则的长等于( ) A、7cm B、6cm C、5cm D、11cm11. 如图,点F为正方形对角线的中点,将以点F为直角顶点的直角绕点F旋转(的边EG始终在正方形外),若正方形边长为3,则在旋转过程中与正方形重叠部分的面积为( )
A、7cm B、6cm C、5cm D、11cm11. 如图,点F为正方形对角线的中点,将以点F为直角顶点的直角绕点F旋转(的边EG始终在正方形外),若正方形边长为3,则在旋转过程中与正方形重叠部分的面积为( ) A、9 B、3 C、4.5 D、2.2512. 已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( )
A、9 B、3 C、4.5 D、2.2512. 已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 在平面直角坐标系中,点与点关于原点对称,则m的值为 .14. 小李在罚球线上投篮结果的频数表如下,则他一次投中的概率是.(精确到0.1)
投篮次数n
50
100
150
200
250
300
500
投中次数m
28
58
78
104
123
152
251
投中频率
0.56
0.580
0.520
0.520
0.492
0.506
0.502
15. 在半径为的圆中,的圆心角所对弧的弧长是.16. 有1个人患了流感,经过两轮传染后共有36人患了流感,那么平均每轮传染 人.17. 如图,在平面直角坐标系中,的顶点、在轴上,、两点分别在反比例函数与的图像上,若的面积为4,则的值为 .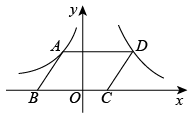 18. 在矩形 中, , 点E在边上, , 点P为矩形内一点且 , 点M为边上一点,连接 , 则的最小值为 .
18. 在矩形 中, , 点E在边上, , 点P为矩形内一点且 , 点M为边上一点,连接 , 则的最小值为 .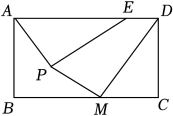
三、解答题
-
19. 计算:.20. 解方程:x2+2x﹣3=0.21. 某景区检票口有A,B,C共3个检票通道,甲,乙两人到该景区游玩,两人分别从3个检票通道中随机选择一个检票.(1)、甲选择A检票通道的概率是 ;(2)、求甲,乙两人选择的检票通道恰好相同的概率.22. 已知如表是反比例函数关于自变量x与函数值y的部分对应值:
x
…
-8
-4
-2
-1
1
2
4
8
…
y
…
-1
m
-4
-8
8
n
2
1
…
 (1)、直接写出k,m,n的值;(2)、根据表中的数值画出反比例函数的图象;(3)、根据图象,当时,直接写出自变量x的取值范围.23. 【提出问题】我们知道,点和圆有三种位置关系(如图1).已知在⊙O中,点A、B、C分别是圆外、圆上、圆内的点,点D、E是上不与点B重合的任意两点,分别连接AD、AE、BD、BE、CD、CE,如何比较、、的大小关系.
(1)、直接写出k,m,n的值;(2)、根据表中的数值画出反比例函数的图象;(3)、根据图象,当时,直接写出自变量x的取值范围.23. 【提出问题】我们知道,点和圆有三种位置关系(如图1).已知在⊙O中,点A、B、C分别是圆外、圆上、圆内的点,点D、E是上不与点B重合的任意两点,分别连接AD、AE、BD、BE、CD、CE,如何比较、、的大小关系.
【解决问题】小邕利用已学知识判断和的大小关系,步骤如下:
解: , 理由如下:
如图2,延长DC与相交于点F,连接EF,由同弧或等弧所对的圆周角相等,可知 ,
∵是△CFE的外角,
∴∠DFE+∠CEF=∠DCE,
∴∠DFE<∠DCE,
∴∠B<∠DCE.
(1)、请参照小邕的解题步骤,比较和的大小关系,并说明理由.(2)、【实践应用】
如图3,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,.为了避免轮船P触礁,轮船P所在的位置与两座灯塔A、B的视角度数的最大值是多少?并说明理由.(3)、2022卡塔尔世界杯正在如火如荼的进行中,全民足球热情高涨.因此某校举办了足球比赛,在其中一场比赛中(如图4),甲带球奔向对方球门 , 当他带球冲到A点时,同伴乙已经冲到B点,同伴丙已经冲到C点.此时有三种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门;第三种是甲将球传给丙,由丙射门.仅从射门角度越大,进球概率越大的角度考虑,请直接写出应选择第几种射门方式.24. 某校为进一步打造“空中花园”,优化育人环境,增添校园绿色文化,计划到一家花卉种植基地采购甲、乙两种花卉共50盆,其中甲种花卉的数量不超过30盆,且不少于10盆.据了解,甲、乙两种花卉的原价分别是80元/盆、56元/盆.种植基地负责人为了支持学校建设,提供以下优惠:购买几盆甲种花卉,甲种花卉每盆就降几元,乙种花卉按原价购买.设该校购买甲种花卉x盆,请回答以下问题:(1)、若该校采购甲、乙两种花卉共花费2880元,求该校分别购买甲、乙两种花卉各多少盆?(2)、设购买甲、乙两种花卉共花费w元,求w与x的函数关系式;(3)、请预计本次采购该校最少准备多少元,最多准备多少元?

