2023年中考数学精选真题实战测试20 函数基础知识 B
试卷更新日期:2023-01-10 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 匀速地向一个容器内注水,最后把容器注满.在注水过程中,水面高度随时间的变化规律如图所示(图中为一折线).这个容器的形状可能是( )
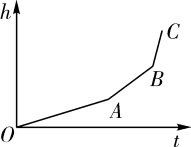 A、
A、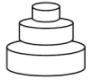 B、
B、 C、
C、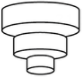 D、
D、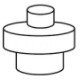 2. 已知函数 , 则自变量的取值范围是( )A、 B、﹣1且 C、 D、3. 变量x,y的一些对应值如下表:
2. 已知函数 , 则自变量的取值范围是( )A、 B、﹣1且 C、 D、3. 变量x,y的一些对应值如下表:…
-2
-1
0
1
2
3
…
…
-1
-0.5
0
0.5
1
1.5
…
根据表格中的数据规律,当时,y的值是( )
A、2 B、-2.5 C、-1.5 D、-24. 甲、乙两人沿同一直道从地到地,在整个行程中,甲、乙离地的距离与时间之间的函数关系如图所示,下列说法错误的是( ) A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地5. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )
A、甲比乙早1分钟出发 B、乙的速度是甲的速度的2倍 C、若甲比乙晚5分钟到达,则甲用时10分钟 D、若甲出发时的速度为原来的2倍,则甲比乙提前1分钟到达地5. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )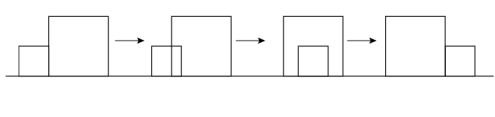 A、
A、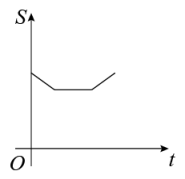 B、
B、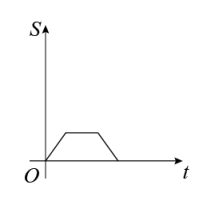 C、
C、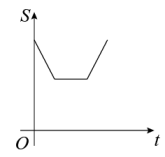 D、
D、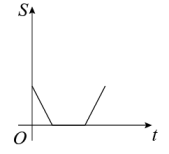 6. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )
6. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )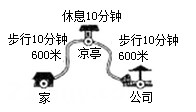 A、
A、 B、
B、 C、
C、 D、
D、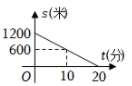 7. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形PQMN的面积为( )
7. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形PQMN的面积为( ) A、16 B、20 C、36 D、458. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( )
A、16 B、20 C、36 D、458. 如图,在▱ABCD中,∠A=60°,AB=2,AD=1,点E,F在▱ABCD的边上,从点A同时出发,分别沿A→B→C和A→D→C的方向以每秒1个单位长度的速度运动,到达点C时停止,线段EF扫过区域的面积记为y,运动时间记为x,能大致反映y与x之间函数关系的图象是( ) A、
A、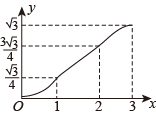 B、
B、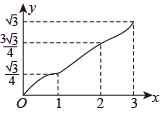 C、
C、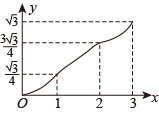 D、
D、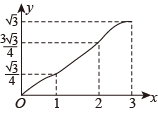 9. 定义一种运算:则函数的图象大致是( )A、
9. 定义一种运算:则函数的图象大致是( )A、 B、
B、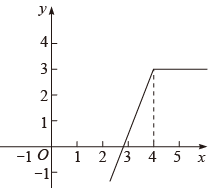 C、
C、 D、
D、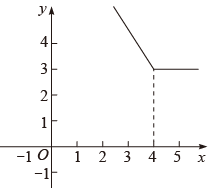 10. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
10. 如图,在中, , 动点P从点A出发,以每秒1个单位长度的速度沿线段匀速运动,当点P运动到点B时,停止运动,过点P作交于点Q,将沿直线折叠得到 , 设动点P的运动时间为t秒,与重叠部分的面积为S,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每空3分,共18分)
-
11. 若函数y= , 则当函数值y=8时,自变量x的值等于.12. 如图,正方形中,点、从点出发,以的速度分别沿和的路径匀速运动,同时到达点时停止运动.连接 , 设的长为 , 运动时间为 , 则与(秒)的函数图象如图所示.当秒时,的长是.
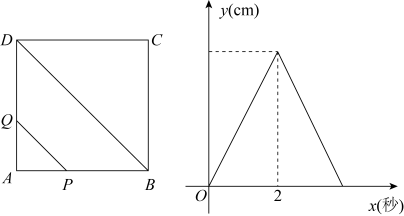 13. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点.
13. 女子10千米越野滑雪比赛中,甲、乙两位选手同时出发后离起点的距离x(千米)与时间(分钟)之间的函数关系如图所示,则甲比乙提前分钟到达终点. 14. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是h.
14. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离甲地的距离y(单位:)与慢车行驶时间t(单位:h)的函数关系如图,则两车先后两次相遇的间隔时间是h. 15. 小亮和小颖两位同学从距离图书馆3000米的同一小区同时出发,各自去还图书,然后再从图书馆借书后原路原速返回自己居住的小区(借书、还书等逗留时间忽略不计),在整个过程中,两位同学的速度均保持匀速行驶,且小亮的速度快于小颖,两人相距的路程 (米)与小亮离开小区的时间 (分)之间的关系如图中折线所示,则点 的坐标为.
15. 小亮和小颖两位同学从距离图书馆3000米的同一小区同时出发,各自去还图书,然后再从图书馆借书后原路原速返回自己居住的小区(借书、还书等逗留时间忽略不计),在整个过程中,两位同学的速度均保持匀速行驶,且小亮的速度快于小颖,两人相距的路程 (米)与小亮离开小区的时间 (分)之间的关系如图中折线所示,则点 的坐标为.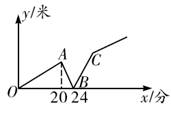 16. 已知函数 ,其中 表示当 时对应的函数值,如 , , ,…, ,则 .
16. 已知函数 ,其中 表示当 时对应的函数值,如 , , ,…, ,则 .三、解答题(共7题,共72分)
-
17. 如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.
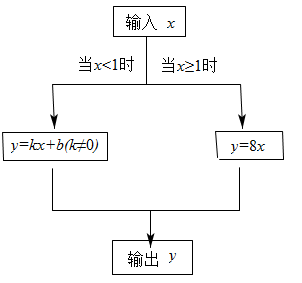
输人x
…
-6
-4
-2
0
2
…
输出y
…
-6
-2
2
6
16
…
根据以上信息,解答下列问题:
(1)、当输入的x值为1时,输出的y值为;(2)、求k,b的值;(3)、当输出的y值为0时,求输入的x值.18. 由于精准扶贫的措施科学得当,贫困户小颖家今年种植的草莓喜获丰收,采摘上市16天全部销售完.小颖对销售情况进行统计后发现,在该草莓上市第x天(x取整数)时,日销售量y(单位:千克)与x之间的函数关系式为草莓价格m(单位:元/千克)与x之间的函数关系如图所示. (1)、求第14天小颖家草莓的日销售量;(2)、求当时,草莓价格m与x之间的函数关系式;(3)、试比较第8天与第10天的销售金额哪天多?19. 甲骑车从A地到B地,乙骑车从B地到A地,甲的速度小于乙的速度,两人同时出发,沿同一条道路骑行,图中的折线表示两人之间的距离y(km)与甲的行驶时间x(h)之间的关系,根据图象回答下列问题:
(1)、求第14天小颖家草莓的日销售量;(2)、求当时,草莓价格m与x之间的函数关系式;(3)、试比较第8天与第10天的销售金额哪天多?19. 甲骑车从A地到B地,乙骑车从B地到A地,甲的速度小于乙的速度,两人同时出发,沿同一条道路骑行,图中的折线表示两人之间的距离y(km)与甲的行驶时间x(h)之间的关系,根据图象回答下列问题: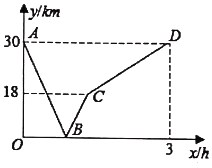 (1)、甲骑完全程用时小时;甲的速度是km/h;(2)、求甲、乙相遇的时间;(3)、求甲出发多长时间两人相距10千米.20. 果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为 . 在确保每棵果树平均产量不低于的前提下,设增种果树x(且x为整数)棵,该果园每棵果树平均产量为 , 它们之间的函数关系满足如图所示的图象.
(1)、甲骑完全程用时小时;甲的速度是km/h;(2)、求甲、乙相遇的时间;(3)、求甲出发多长时间两人相距10千米.20. 果园有果树60棵,现准备多种一些果树提高果园产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵果树时,果园内的每棵果树平均产量为 . 在确保每棵果树平均产量不低于的前提下,设增种果树x(且x为整数)棵,该果园每棵果树平均产量为 , 它们之间的函数关系满足如图所示的图象.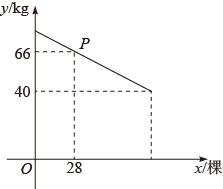 (1)、图中点P所表示的实际意义是 , 每增种1棵果树时,每棵果树平均产量减少;(2)、求y与x之间的函数关系式,并直接写出自变量x的取值范围;(3)、当增种果树多少棵时,果园的总产量最大?最大产量是多少?21. 如图1,在 中, , , .点D从A点出发,沿线段AB向终点B运动.过点D作AB的垂线,与 的直角边AC(或BC)相交于点E.设线段AD的长为a(cm),线段DE的长为h(cm).
(1)、图中点P所表示的实际意义是 , 每增种1棵果树时,每棵果树平均产量减少;(2)、求y与x之间的函数关系式,并直接写出自变量x的取值范围;(3)、当增种果树多少棵时,果园的总产量最大?最大产量是多少?21. 如图1,在 中, , , .点D从A点出发,沿线段AB向终点B运动.过点D作AB的垂线,与 的直角边AC(或BC)相交于点E.设线段AD的长为a(cm),线段DE的长为h(cm).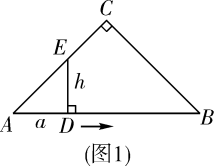 (1)、为了探究变量a与h之间的关系,对点D在运动过程中不同时刻AD,DE的长度进行测量,得出以下几组数据:
(1)、为了探究变量a与h之间的关系,对点D在运动过程中不同时刻AD,DE的长度进行测量,得出以下几组数据:变量a(cm)
0
0.5
1
1.5
2
2.5
3
3.5
4
变量h(cm)
0
0.5
1
1.5
2
1.5
1
0.5
0
在平面直角坐标系中,以变量a的值为横坐标,变量h的值为纵坐标,描点如图2-1;以变量h的值为横坐标,变量a的值为纵坐标,描点如图2-2.
根据探究的结果,解答下列问题:
①当 时, ▲ ;当 时, ▲ .
②将图2-1,图2-2中描出的点顺次连接起来.
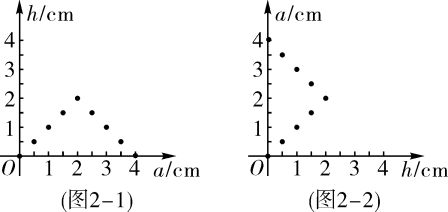
③下列说法正确的是 ▲ .(填“A”或“B”)
A.变量h是以a为自变量的函数 B.变量a是以h为自变量的函数
(2)、如图3,记线段DE与 的一直角边、斜边围成的三角形(即阴影部分)的面积 为s.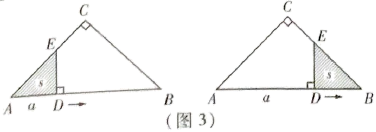
①分别求出当 和 时,s关于a的函数表达式;
②当 时,求a的值.
22. 共享科技深入人心,也方便了百姓的生活,共享洗车是共享科技下的一种洗车方式,如图是普通洗车收费和共享洗车收费与洗车时间的函数图象,请根据图像回答相关问题. (1)、共享洗车方式段单价为元/ , 洗车时间为时,两种洗车方式收费相同.(2)、求段关于的函数表达式.(3)、当两种洗车方式收费差距在2元(包含2元)内时,求共享洗车时间的取值范围.23. 甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶.
(1)、共享洗车方式段单价为元/ , 洗车时间为时,两种洗车方式收费相同.(2)、求段关于的函数表达式.(3)、当两种洗车方式收费差距在2元(包含2元)内时,求共享洗车时间的取值范围.23. 甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶. (1)、填空:
(1)、填空:① 两城相距 ;
②当 时,甲车的速度为 ;
③乙车比甲车晚 到达 城;
④甲车出发 时,距离 城 ;
⑤甲、乙两车在行程中相遇时,甲车离开 城的时间为 ;
(2)、当 时,请直接写出 关于 的函数解析式.(3)、当 时,两车所在位置的距离最多相差多少 ?