2023年中考数学精选真题实战测试19 函数基础知识 A
试卷更新日期:2023-01-10 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为 .下列判断正确的是( )A、2是变量 B、 是变量 C、r是变量 D、C是常量2. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且3. 中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系:折线表示轿车离西昌距离与时间之间的函数关系,则以下结论错误的是( )
 A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km4. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、
A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km4. 2022年2月5日,电影《长津湖》在青海剧场首映,小李一家开车去观看.最初以某一速度匀速行驶,中途停车加油耽误了十几分钟,为了按时到达剧场,小李在不违反交通规则的前提下加快了速度,仍保持匀速行驶.在此行驶过程中,汽车离剧场的距离y(千米)与行驶时间t(小时)的函数关系的大致图象是( )A、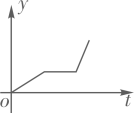 B、
B、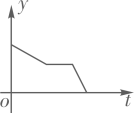 C、
C、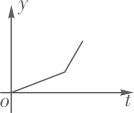 D、
D、 5. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )
5. 遵义市某天的气温(单位:℃)随时间t(单位:h)的变化如图所示,设表示0时到t时气温的值的极差(即0时到时范围气温的最大值与最小值的差),则与t的函数图象大致是( )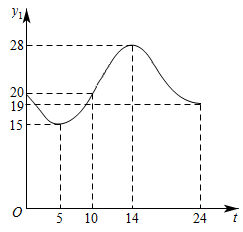 A、
A、 B、
B、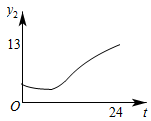 C、
C、 D、
D、 6. 下列曲线中不能表示y与x的函数的是( )A、
6. 下列曲线中不能表示y与x的函数的是( )A、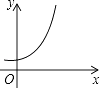 B、
B、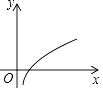 C、
C、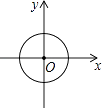 D、
D、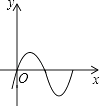 7. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣18. 下面的三个问题中都有两个变量:
7. 已知y1和y2均是以x为自变量的函数,当x=n时,函数值分别是N1和N2 , 若存在实数n,使得N1+N2=1,则称函数y1和y2是“和谐函数”.则下列函数y1和y2不是“和谐函数”的是( )A、y1=x2+2x和y2=﹣x+1 B、y1=和y2=x+1 C、y1=﹣和y2=﹣x﹣1 D、y1=x2+2x和y2=﹣x﹣18. 下面的三个问题中都有两个变量:①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x,其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )
 A、①② B、①③ C、②③ D、①②③9. 如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )
A、①② B、①③ C、②③ D、①②③9. 如图①所示(图中各角均为直角),动点Р从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积y随点Р运动的时间x(秒)之间的函数关系图象如图②所示,下列说法正确的是( )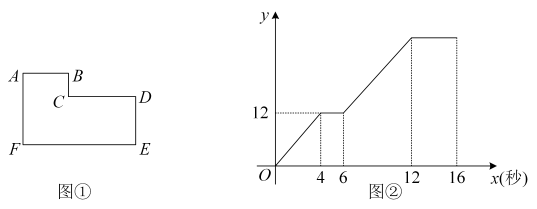 A、AF=5 B、AB=4 C、DE=3 D、EF=810. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )
A、AF=5 B、AB=4 C、DE=3 D、EF=810. 如图,△ABC中,BC=6,BC边上的高为3,点D,E,F分别在边BC,AB,AC上,且EF∥BC.设点E到BC的距离为x,△DEF的面积为y,则y关于x的函数图象大致是( )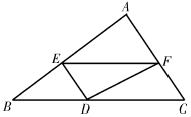 A、
A、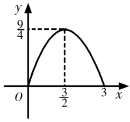 B、
B、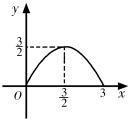 C、
C、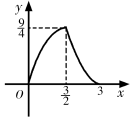 D、
D、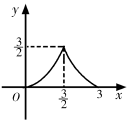
二、填空题(每空3分,共18分)
-
11. 周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a= .
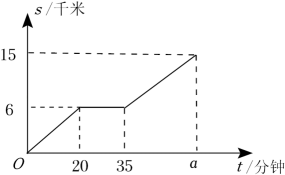 12. 已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是 . (填写所有正确结论的序号)
12. 已知王强家、体育场、学校在同一直线上,下面的图像反映的过程是:某天早晨,王强从家跑步去体育场锻炼,锻炼结束后,步行回家吃早餐,饭后骑自行车到学校.图中表示时间,表示王强离家的距离.则下列结论正确的是 . (填写所有正确结论的序号)①体育场离王强家
②王强在体育场锻炼了
③王强吃早餐用了
④王强骑自行车的平均速度是
 13. 已知函数y= ,若y=2,则x=.14. 小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是千米.
13. 已知函数y= ,若y=2,则x=.14. 小韦同学周末的红色之旅,坐爸爸的车去百色起义纪念馆,从家里行驶7千米后,进入高速公路,在高速公路上保持匀速行驶,小韦记录高速公路上行驶的时间(和路程)数据如下表,按照这个速度行驶了2小时进入高速路出口匝道,再行驶5千米抵达纪念馆,则小韦家到纪念馆的路程是千米.t小时
0.2
0.6
0.8
s千米
20
60
80
15. 如图1,△ABC中,∠ABC=60°,D是BC边上的一个动点(不与点B,C重合),DEAB,交AC于点E,EFBC,交AB于点F.设BD的长为x,四边形BDEF的面积为y,y与x的函数图象是如图2所示的一段抛物线,其顶点P的坐标为(2,3),则AB的长为 .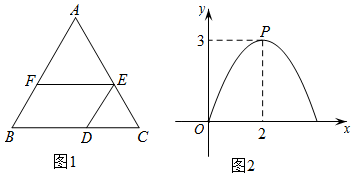 16. 如图1,在中, , 动点从点出发,沿折线匀速运动至点停止.若点的运动速度为 , 设点的运动时间为 , 的长度为 , 与的函数图象如图2所示.当恰好平分时的值为.
16. 如图1,在中, , 动点从点出发,沿折线匀速运动至点停止.若点的运动速度为 , 设点的运动时间为 , 的长度为 , 与的函数图象如图2所示.当恰好平分时的值为.
三、解答题(共7题,共72分)
-
17. 探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有经验,请画出函数y=-|x|的图象,并探究该函数性质.(1)、绘制函数图象
①列表:下列是x与y的几组对应值,其中a= ▲ .
x
……
﹣5
﹣4
﹣3
﹣2
﹣1
1
2
3
4
5
……
y
……
﹣3.8
﹣2.5
﹣1
1
5
5
a
﹣1
﹣2.5
﹣3.8
……
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
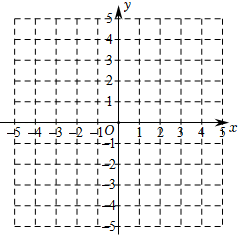 (2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质
(2)、探究函数性质,请写出函数y=-|x|的一条性质:;(3)、运用函数图象及性质①写出方程-|x|=5的解;
②写出不等式-|x|≤1的解集 .
18. 为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
 (1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?19. 在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示:
(1)、在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;(2)、在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)、该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?19. 在“看图说故事”话动中,某学习小组设计了一个问题情境:小明从家跑步去体育场,在那里锻炼了一阵后又走到文具店买圆规,然后散步走回家.小明离家的距离y(km)与他所用的时间x(min)的关系如图所示: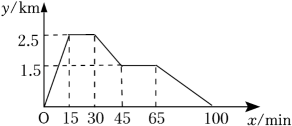 (1)、小明家离体育场的距离为km,小明跑步的平均速度为km/min;(2)、当15≤x≤45时,请直接写出y关于x的函数表达式;(3)、当小明离家2km时,求他离开家所用的时间.20. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:
(1)、小明家离体育场的距离为km,小明跑步的平均速度为km/min;(2)、当15≤x≤45时,请直接写出y关于x的函数表达式;(3)、当小明离家2km时,求他离开家所用的时间.20. 6月13日,某港口的湖水高度y(cm)和时间x(h)的部分数据及函数图象如下:x(h)
…
11
12
13
14
15
16
17
18
…
Y(cm
…
189
137
103
80
101
133
202
260
…
(数据来自某海洋研究所)
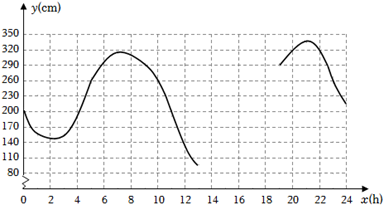 (1)、数学活动:
(1)、数学活动:①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
(2)、数学思考:请结合函数图象,写出该函数的两条性质或结论.
(3)、数学应用:根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
21. 已知A、B两地之间有一条长440千米的高速公路.甲、乙两车分别从A、B两地同时出发,沿此公路相向而行,甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇,再以另一速度继续匀速行驶4小时到达B地;乙车匀速行驶至A地,两车到达各自的目的地后停止.两车距A地的路程y(千米)与各自的行驶时间x(时)之间的函数关系如图所示.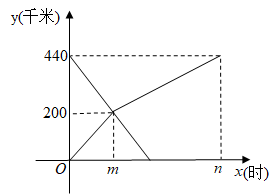 (1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.22. 为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.
(1)、m= , n=;(2)、求两车相遇后,甲车距A地的路程y与x之间的函数关系式;(3)、当乙车到达A地时,求甲车距A地的路程.22. 为抗击疫情,支援B市,A市某蔬菜公司紧急调运两车蔬菜运往B市.甲、乙两辆货车从A市出发前往B市,乙车行驶途中发生故障原地维修,此时甲车刚好到达B市.甲车卸载蔬菜后立即原路原速返回接应乙车,把乙车的蔬菜装上甲车后立即原路原速又运往B市.乙车维修完毕后立即返回A市.两车离A市的距离y(km)与乙车所用时间x(h)之间的函数图象如图所示.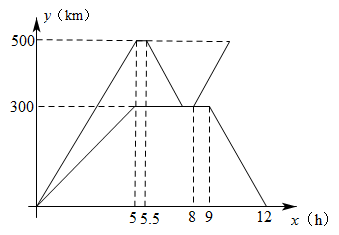 (1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.23. 在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题:
(1)、甲车速度是km/h,乙车出发时速度是km/h;(2)、求乙车返回过程中,乙车离A市的距离y(km)与乙车所用时间x(h)的函数解析式(不要求写出自变量的取值范围);(3)、乙车出发多少小时,两车之间的距离是120km?请直接写出答案.23. 在一条笔直的公路上有A、B两地,甲、乙二人同时出发,甲从A地步行匀速前往B地,到达B地后,立刻以原速度沿原路返回A地.乙从B地步行匀速前往A地(甲、乙二人到达A地后均停止运动),甲、乙二人之间的距离y (米)与出发时间x (分钟)之间的函数关系如图所示,请结合图像解答下列问题: (1)、A、B两地之间的距离是米,乙的步行速度是米/分;(2)、图中a= , b= , c= ;(3)、求线段MN的函数解析式;(4)、在乙运动的过程中,何时两人相距80米?(直接写出答案即可)
(1)、A、B两地之间的距离是米,乙的步行速度是米/分;(2)、图中a= , b= , c= ;(3)、求线段MN的函数解析式;(4)、在乙运动的过程中,何时两人相距80米?(直接写出答案即可)