2023年浙教版数学八年级下册第一章二次根式（基础版）

试卷更新日期：2023-01-09 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列各式是二次根式的是（）

A、 $\sqrt{- 2}$ B、 $- \sqrt{2}$ C、 $\sqrt[3]{2}$ D、 $\sqrt{x}$

查看试题解析
2. 代数式 $\sqrt{x + 1}$ 在实数范围内有意义，则实数x的取值范围是（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x \leq - 1$ D、 $x \geq - 1$

查看试题解析
3. 化简二次根式 $- \sqrt{8 a^{3}}$ 的结果为（）

A、 $2 a \sqrt{2 a}$ B、 $- 2 \sqrt{2 a^{3}}$ C、 $2 a \sqrt{- 2 a}$ D、 $- 2 a \sqrt{2 a}$

查看试题解析
4. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{13}$ C、 $\sqrt{27}$ D、 $\sqrt{\frac{4}{3}}$

查看试题解析
5. 下列各式中与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $2 \sqrt{3}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
6. 下列等式：① $\sqrt{\frac{1}{16}} = \frac{1}{8}$ ，② $\sqrt[3]{{(- 2)}^{3}} = - 2$ ，③ $\sqrt{{(- 2)}^{2}} = 2$ ，④ $\sqrt[3]{- 8} = - \sqrt[3]{8}$ ⑤ $\sqrt{16} = \pm 4$ ，⑥ $- \sqrt{4} = - 2$ ；正确的有（）个

A、5个 B、4个 C、3个 D、2个

查看试题解析
7. 若 $\sqrt{x + 6} + \sqrt{2 + y}$ =0，则 $\sqrt{x y}$ =（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、 $- 2 \sqrt{2}$ D、 $- 2 \sqrt{3}$

查看试题解析
8. 下列计算中，正确的是（）

A、 $\sqrt{5} - \sqrt{3} = \sqrt{2}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\sqrt{8} \div \sqrt{2} = 2$ D、 $\sqrt{(- 3)^{2}} = - 3$

查看试题解析
9. $\sqrt{3}$ 的倒数是（）

A、 $- \sqrt{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、-3 D、 $\frac{\sqrt{3}}{3}$

查看试题解析
10. 如图，在长方形 $A B C D$ 中无重叠放入面积分别为 $12 c m^{2}$ 和 $16 c m^{2}$ 的两张正方形纸片，则图中空白部分的面积为（）

A、 $8 - 4 \sqrt{3}$ B、 $16 - 8 \sqrt{3}$ C、 $8 \sqrt{3} - 12$ D、 $4 - 2 \sqrt{3}$

查看试题解析

二、填空题（每题4分，共24分）

11. 函数 $y = \frac{\sqrt{x - 3}}{x + 5}$ 中，自变量x的取值范围是．

查看试题解析
12. 在二次根式 $\sqrt{15}$ ， $\sqrt{20}$ ， $\sqrt{\frac{2}{3}}$ ， $\sqrt{0.4}$ 中，最简二次根式有个．

查看试题解析
13. 如果最简二次根式 $\sqrt{x + 3}$ 与最简二次根式 $\sqrt{1 + 2 x}$ 是同类二次根式，则 $x =$ ．

查看试题解析
14. 已知 $\sqrt{{(x - 5)}^{2}} = 5 - x$ ，则x的取值范围是．

查看试题解析
15. 计算： $\sqrt{3} \div \sqrt{6}$ =

查看试题解析
16. 已知实数a在数轴上的位置如图所示，则化简 $\sqrt{{(a - 2)}^{2}} =$ ．

查看试题解析

三、解答题（共8题，共66分）

17. 当x分别取下列值时，求二次根式 $\sqrt{9 - 8 x}$ 的值．

(1)、x=0；

(2)、x= $\frac{1}{2}$ ；

(3)、x= -2．

查看试题解析
18. 计算：

(1)、 $(- \sqrt{3})^{2} + \sqrt{32} - 2 \sqrt{4 \frac{1}{2}}$ ；

(2)、 $\sqrt{27} \times \sqrt{50} \div \sqrt{6}$ ；

(3)、 $\sqrt{48} - (\sqrt{3} + 1)^{2} + \sqrt{\frac{3}{4}}$ ；

(4)、 $(3 + 2 \sqrt{2}) (3 - 2 \sqrt{2})$ ．

查看试题解析
19. 已知 $x = \sqrt{7} + \sqrt{5}$ ， $y = \sqrt{7} - \sqrt{5}$ ，求下列各式的值

(1)、 $x^{2} - x y + y^{2}$

(2)、 $\frac{x}{y} - \frac{y}{x}$ ．

查看试题解析
20. 若实数a满足 $| 2019 - a | + \sqrt{a - 2020} = a$ ，求a-2019²的值．

查看试题解析
21. 先化简，再求值： $a + \sqrt{1 - 2 a + a^{2}}$ ，其中 $a = 2020$ .如图是小亮和小芳的解答过程.

(1)、的解法是错误的；
错误的原因在于未能正确地运用二次根式的性质：；

(2)、先化简，再求值： $a + 2 \sqrt{a^{2} - 8 a + 16}$ ，其中 $a = - 2021$ .

查看试题解析
22. 已知a，b分别为等腰三角形的两条边长，且a，b满足b＝4＋ $\sqrt{3 a - 6}$ ＋3 $\sqrt{2 - a}$ ，求此三角形的周长.

查看试题解析
23. 古希腊的几何学家海伦给出了求三角形面积的公式：S= $\sqrt{p (p - a) (p - b) (p - c)}$ ，其中a，b，c为三角形的三边长，p= $\frac{a + b + c}{2}$ ．若一个三角形的三边长分别为2，3，4，求该三角形的面积．

查看试题解析
24. 如图，在△ABC中，∠ACB=90°，CD⊥_AB于点D，AC+BC= $\sqrt{6} + \sqrt{2}$ ，AB=2 $\sqrt{2}$ ．

(1)、求△ABC的面积；

(2)、求CD的长．

查看试题解析
25. 【观察】
$\frac{1}{\sqrt{3}} = \frac{1 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
【感悟】
在二次根式的运算中，需要运用分式的基本性质，将分母转化为有理数，这就是分母有理化．像上述解题过程中 $\sqrt{3}$ 与 $\sqrt{3}$ ， $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ 相乘的积都不含二次根式，我们可以将这两个式子称为互为有理化因式．

(1)、【运用】 $\sqrt{2}$ 的有理化因式是； $\sqrt{3} - 2$ 的有理化因式是；

(2)、将下列各式分母有理化：
① $\frac{1}{\sqrt{5} + 2}$ ；
② $\frac{2}{\sqrt{3} - \sqrt{5}}$

查看试题解析
26. 为了打赢湖北保卫战、武汉保卫战，4万多名医护人员逆行出征，约4万名建设者从八方赶来，并肩奋战，抢建火神山和雷神山医院．他们日夜鏖战，与病毒竞速，创造了10天左右时间建成两座传染病医院的“中国速度”！他们不畏风险，同困难斗争，充分展现团结起来打硬仗的“中国力量”，在建设过程中，有一位木工遇到了这样一道数学题：
有一块矩形木板，木工采用如图的方式，在木板上截出两个面积分别为 $18 d m^{2}$ 和 $32 d m^{2}$ 的正方形木板．

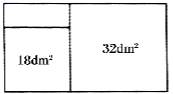(1)、求剩余木料的面积？

(2)、如果木工想从剩余的木料中截出长为 $1.5 d m$ ，宽为 $1 d m$ 的长方形木条，最多能截出块这样的木条．

查看试题解析

2023年浙教版数学八年级下册第一章 二次根式（基础版）

一、单选题（每题3分，共30分）

二、填空题（每题4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学八年级下册第一章二次根式（基础版）