2023年浙教版数学八年级下册1.3 二次根式的运算 同步测试
试卷更新日期:2023-01-09 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列各式中,不成立的是( )A、 B、 C、 D、3. 下列各组二次根式,是同类二次根式的是( )A、与 B、与 C、与 D、与4. 估计 的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间5. 若+2 +=10,则x的值为( )A、4 B、±4 C、2 D、±26. 实数a、b在数轴上对应的位置如图,则 ( )
 A、b-a B、2-a-b C、a-b D、2+a-b7. 一个长方体的体积是 ,长是 ,宽是 ,则它的高是( )A、 B、 C、 D、8. 在化简时,甲、乙两位同学的解答如下:
A、b-a B、2-a-b C、a-b D、2+a-b7. 一个长方体的体积是 ,长是 ,宽是 ,则它的高是( )A、 B、 C、 D、8. 在化简时,甲、乙两位同学的解答如下:甲:;
乙:.
这两位同学的解法,你认为( )
A、两人解法都对 B、甲错乙对 C、甲对乙错 D、两人都错9. 如图,在一个长方形中无重叠的放入面积分别为和的两张正方形纸片,则图中空白部分的面积为( )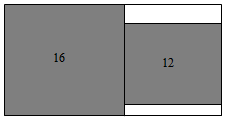 A、 B、 C、 D、10. 我国宋代数学家秦九韶和古希腊几何学家海伦都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为a,b,c,若 , , ,则 的面积为( )
A、 B、 C、 D、10. 我国宋代数学家秦九韶和古希腊几何学家海伦都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为a,b,c,若 , , ,则 的面积为( )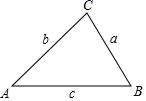 A、 B、 C、24 D、
A、 B、 C、24 D、二、填空题(每题3分,共18分)
-
11. 若与最简二次根式是同类二次根式,则 .12. 计算的结果为 .13. 已如 , . 则 .14. 已知 , 则的值为 .15. 分母有理化:= .16. 在中,已知 , , 则其周长为 .
三、解答题(共10题,共72分)
-
17. 计算(1)、(2)、(3)、(4)、18. 已知等式成立,化简|x-6|+的值.19. 已知在△ABC中,∠C=90°,BC=2+1,AC=2-1,求AB的长.20.(1)、计算: .(2)、下面是夏红同学对题目的计算过程,请认真阅读并完成相应的任务.
题目:已知 , 求的值.
原式第一步
第二步
第三步
所代入上式,得
原式 第四步
第五步
. 第六步
任务一:填空:
①在化简步骤中,第步是进行分式的通分.
②第步开始出错,这一错误的原因是 .
任务二:请直接写出该题计算后的正确结果 .
21. 像 , , 两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如:与 , 与 , 与等都是互为有理化因式,进行二次根式计算时,利用有理化因式,可以化去分母中的根号,请回答下列问题:(1)、化简:①= ;②= .(2)、计算: .22. 小明家装修,电视背景墙长BC为 m,宽AB为 m,中间要镶一个长为2 m宽为 m的长方形大理石图案(图中阴影部分).除去大理石图案部分,其他部分贴壁布,求壁布的面积(结果化为最简二次根式) 23. 阅读下列材料,然后回答问题.
23. 阅读下列材料,然后回答问题.在进行二次根式运算时,我们有时会碰上这样的式子,其实我们还可以将其进一步化简:
(Ⅰ) .
以上这种化简的步骤叫作分母有理化.
(Ⅱ)还可以用以下方法化简
.
(1)、请用不同的方法化简 .①参照(Ⅰ)式,化简;
②参照(Ⅱ)式,化简;
(2)、化简:24. 已知 中, , , .(1)、分别化简 , ;(2)、试在4×4的方格纸上画出 ,使它的顶点都在方格的顶点上(每个小方格的边长为1);并求点B到 边的距离.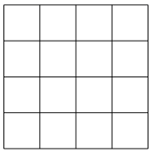 25. 同学们学过数轴知道数轴上点与实数一一对应,在一条不完整的数轴上从左到右有点A,B,C,其中 , , 如图所示,设点A,B,C所对应数的和是P.
25. 同学们学过数轴知道数轴上点与实数一一对应,在一条不完整的数轴上从左到右有点A,B,C,其中 , , 如图所示,设点A,B,C所对应数的和是P.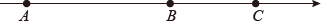 (1)、若以B为原点,写出点A,C所对应的数,并计算P的值;(2)、若原点为O且 , 求P的值.26. 高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式t= (不考虑风速的影响).(1)、从50m高空抛物到落地所需时间t1是多少s,从100m高空抛物到落地所需时间t2是多少s;(2)、t2是t1的多少倍?(3)、经过1.5s,高空抛物下落的高度是多少?
(1)、若以B为原点,写出点A,C所对应的数,并计算P的值;(2)、若原点为O且 , 求P的值.26. 高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式t= (不考虑风速的影响).(1)、从50m高空抛物到落地所需时间t1是多少s,从100m高空抛物到落地所需时间t2是多少s;(2)、t2是t1的多少倍?(3)、经过1.5s,高空抛物下落的高度是多少?