(人教版)2022-2023学年七年级数学下册6.3实数 同步测试
试卷更新日期:2023-01-09 类型:同步测试
一、单选题
-
1. 已知 , 介于两个连续自然数之间,则下列选项正确的是( )A、 B、 C、 D、2. 下列实数中,无理数是( )A、0 B、3.14 C、 D、3. 已知数a,b,c的大小关系如图所示,则下列各式:
①;②;③;④ , 其中正确个数是( )
 A、1 B、2 C、3 D、44. 下面几个数: , 每两个“1之间依次多个0” , , , , , 其中无理数的个数有( )A、1 B、2 C、3 D、45. 估计的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 关于的叙述正确的是( )A、在数轴上不存在表示的点 B、 C、 D、与最接近的整数是37. 在、5、-3π、8.1、1.41414141中,有理数有( )A、1个 B、2个 C、3个 D、4个8. 如果实数a= , 且a在数轴上对应点的位置如图所示,其中正确的是( )A、
A、1 B、2 C、3 D、44. 下面几个数: , 每两个“1之间依次多个0” , , , , , 其中无理数的个数有( )A、1 B、2 C、3 D、45. 估计的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 关于的叙述正确的是( )A、在数轴上不存在表示的点 B、 C、 D、与最接近的整数是37. 在、5、-3π、8.1、1.41414141中,有理数有( )A、1个 B、2个 C、3个 D、4个8. 如果实数a= , 且a在数轴上对应点的位置如图所示,其中正确的是( )A、 B、
B、 C、
C、 D、
D、 9. 下列四个实数中,最大的数是( )A、-3 B、-1 C、 D、310. 实数a,b在数轴上对应点的位置如图所示,下列结论正确的是( )
9. 下列四个实数中,最大的数是( )A、-3 B、-1 C、 D、310. 实数a,b在数轴上对应点的位置如图所示,下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 请你写出一个比1大且比2小的无理数,该无理数可以是.12. 已知 , 是两个连续整数,且满足 , 则的值为.13. 点A,B在数轴上,以AB为边作正方形,该正方形的面积是7.若点A对应的数是-2,则点B对应的数是 .
 14. 如图,直径为1个单位长度的圆,在数轴上从表示的点A滚动一周到点B,则点B表示的无理数为 .
14. 如图,直径为1个单位长度的圆,在数轴上从表示的点A滚动一周到点B,则点B表示的无理数为 . 15. 比较大小:(填“>”或“<”或“=”) .
15. 比较大小:(填“>”或“<”或“=”) .三、解答题
-
16. 把下列各数填入相应的括号内:
正数集合:( …)
整数集合:( …)
负分数集合:( …)
无理数集合:( …)
17. 把下列各数:-2.5,0, , 在数轴上表示出来,并将这些数用“”连接.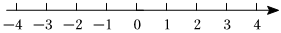 18. 已知的算术平方根是2,的立方根是3,c是的整数部分,求的平方根.
18. 已知的算术平方根是2,的立方根是3,c是的整数部分,求的平方根.四、综合题
-
19. 对于任何实数 , 可用表示不超过的最大整数,如.(1)、则;;(2)、现对119进行如下操作: , 这样对119只需进行3次操作后变为1.
对15进行1次操作后变为 ▲ , 对200进行3次操作后变为 ▲ ;
对实数恰进行2次操作后变成1,则最小可以取到 ▲ ;
若正整数进,3次操作后变为1,求的最大值.
20. 阅读下面的文字,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如: , 即的整数部分为2,小数部分为.
请解答:
(1)、 的整数部分是 , 小数部分是.(2)、已知的小数部分为的小数部分为 , 计算的值.21. 阅读材料,解答下面的问题:, 即 ,
的整数部分为2,小数部分为 .
(1)、求的整数部分.(2)、已知的小数部分是 , 的小数部分是 , 求的值.22. 阅读材料:求1+2+22+23+……+2100的值.解:设S=1+2+22+23+……+2100
将等式两边同时乘以2得
2S=2+22+23+24……+2101
因此2S-S=(2+22+23+24……+2101) - (1+2+22+23+……+2100) =2101-1
所以S=2101-1
即1+2+22+23+……+2100=2101-1
请你仿照此法计算:
(1)、1+2+22+23+24+25=(2)、求1+3+32+……+3101的值.23. 先阅读下面材料,再解答问题:材料:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:若 , 其中a,b为有理数,是无理数,则.
证明:∵ , a为有理数
∴是有理数
∵b为有理数,是无理数
∴
∴
∴
(1)、若 , 其中a、b为有理数,请猜想a= , b= , 并根据以上材料证明你的猜想;(2)、已知的整数部分为a,小数部分为b,且x,y为有理数,x,y,a,b满足 , 求x,y的值.